量子力学视角下的核磁共振波谱（Part 1：量子力学预备知识） | 克莱门森的实验室

0. 前言

本系列文章根据笔者对量子力学和核磁共振的学习经验与感悟总结而得，可以视为对核磁共振物理图景较为粗略浅显的描述。按照笔者的规划，预计至少应有三个部分。

在第一部分，笔者主要对量子力学的知识点进行归纳汇总，为之后磁矢量与积算符的引入打下数学物理基础。而之后的第二部分，则从核磁共振中的自旋现象出发，首先引入核磁自旋的唯象模型，随后指出唯象模型在面对部分分子体系时，缺乏坚实可信，且易于理解的诠释，因此，采用类似于角动量算符形式的积算符，来描述磁矢量随外磁场与射频脉冲的变化，也就变得顺理成章。最后的第三部分，笔者主要结合一些常见的核磁脉冲序列，讲解射频脉冲是如何按一定顺序排列组合，达到测定所需核磁信号的目的。

I. 量子力学预备知识

[I-1] 量子力学基本假设

i. 定义与研究对象初始或边界条件完全相同的电子所构成的集合为“体系”或“系综”，则任意给定体系的一种确定的状态，与线性矢量空间中一束确定的具有相同方向的矢量相对应，该矢量称为体系相应状态的态矢量，简称态矢;
ii. 体系的物理可观测量对应于一定的厄米算符，该算符的本征矢构成相应线性空间的完备基组;
iii. （哥本哈根诠释）对体系的一个物理状态$| u \rangle$，若用算符$\hat{A}$进行测量，则将得到$\hat{A}$的某个本征值$a_i$，并使原来的状态$| u \rangle$投影为$| a_i \rangle$，这一事件发生的概率为$P_i=\big| \langle a_i | u \rangle \big|^2$;
iv. （对易关系）位置算符与动量算符间的基本对易关系为$[\hat{r}_i,\hat{p}_j]=\delta_{ij} \mathrm{i} \hbar \; (i,j=x,y,z)$，其中$\delta_{ij}$为克罗内克记号.

[I-2] 量子力学的两种基本算符——位置算符和动量算符

在经典图景下，任意物体的运动状态均具有两种描述量——位置和速度（或动量），且两者可同时确定。考虑到量子力学必须在体系大小渐近至宏观时，收敛为牛顿力学，因此，量子力学中也应该有位置算符和动量算符，且在经典极限下过渡为牛顿力学的表示方式。

根据量子力学的基本假设i，一维几何空间中粒子的位置$x$对应于态矢$| x \rangle$，而根据基本假设ii，存在位置算符$\hat{x}$，满足$\hat{x} | x \rangle=x | x \rangle$。这样，我们可以将一维几何空间中的任意态矢$| u \rangle$，用位置基矢$| x \rangle$展开，得

$$| u \rangle=\int^{+\infty}_{-\infty} | x \rangle \langle x | u \rangle dx$$

记$\psi(x)=\langle x | u \rangle$，该函数即为位置空间下的波函数，按照基本假设iii，体系处于$x$附近的$dx$区域内的概率为

$$P(x) dx=\big| \langle x | u \rangle \big|^2 dx=\psi^{*}(x) \psi(x) dx$$

特别的，若$| u \rangle$为位置空间的另一基矢$| x’ \rangle$，则用位置基矢$| x \rangle$展开，将变为

$$| x' \rangle=\int^{+\infty}_{-\infty} | x \rangle \langle x | x' \rangle dx=\int^{+\infty}_{-\infty} | x \rangle \delta(x'-x) dx$$

上述的$\delta(x’-x)$为狄拉克delta函数，可认为是连续谱的克罗内克记号，其满足以下性质：

i. $\int^{+\infty}_{-\infty} \delta(x) dx=1$;
ii. $x \neq 0$时，$\delta(x)=0$;
iii. $\int^{+\infty}_{-\infty} f(x) \delta(x-a) dx=f(a)$;
证明：$\int^{+\infty}_{-\infty} f(x) \delta(x-a) dx=\int^{a+\epsilon}_{a-\epsilon} f(x) \delta(x-a) dx=f(a_0) \int^{a+\epsilon}_{a-\epsilon} \delta(x-a) dx=f(a_0)$，其中$a-\epsilon \leq a_0 \leq a+\epsilon$，当$\epsilon \rightarrow 0$时，$f(a_0) \rightarrow f(a)$，证毕.
证明中的第一个等号利用性质ii，第二个等号利用积分中值定理，第三个等号利用性质i.
iv. $\delta(ax)=\frac{\delta(x)}{|a|} \; (a \neq 0)$，特别的，$a=-1$时，有$\delta(x)=\delta(-x)$，即delta函数为偶函数;
证明：$a>0$时，由性质iii得

$$\scriptsize \int^{+\infty}_{-\infty} f(x) \delta(x) dx=f(0) \\ \scriptsize \int^{+\infty}_{-\infty} f(x) \delta(ax) dx=\int^{+\infty}_{-\infty} \frac{f(ax)}{a} \delta(ax) d(ax)=\frac{f(0)}{a}$$

比较两式得$\int^{+\infty}_{-\infty} f(x) \delta(x) dx=\int^{+\infty}_{-\infty} f(x) \frac{\delta(ax)}{a} dx$，即$\delta(ax)=\frac{\delta(x)}{a}$;
$a<0$时，同理可得

$$\scriptsize \int^{+\infty}_{-\infty} f(x) \delta(ax) dx=\int^{-\infty}_{+\infty} \frac{f(ax)}{a} \delta(ax) d(ax)=-\frac{f(0)}{a}$$

比较两式得$\int^{+\infty}_{-\infty} f(x) \delta(x) dx=\int^{+\infty}_{-\infty} f(x) \big[ -\frac{\delta(ax)}{a} \big] dx$，即$\delta(ax)=-\frac{\delta(x)}{a}$;
综上，$\delta(ax)=\frac{\delta(x)}{|a|} \; (a \neq 0)$，证毕;

类似的，一维几何空间中粒子的动量$p$对应于态矢$| p \rangle$，并有相应的算符$\hat{p}$，使$\hat{p} | p \rangle=p | p \rangle$。仿照位置空间的结论，我们有

$$| u \rangle=\int^{+\infty}_{-\infty} | p \rangle \langle p | u \rangle dp=\int^{+\infty}_{-\infty} | p \rangle \varphi(p) dp \\ P(p) dp=\big| \langle p | u \rangle \big|^2 dp=\varphi^{*}(p) \varphi(p) dp \\ | p' \rangle=\int^{+\infty}_{-\infty} | p \rangle \langle p | p' \rangle dp=\int^{+\infty}_{-\infty} | p \rangle \delta(p'-p) dp$$

[I-3] 量子力学的平移算符

通常，我们更喜欢在位置空间（而非动量空间）下描述微观粒子的状态，因此常见的做法是将位置空间变换到坐标空间，同时将动量算符表述为适用于位置空间的形式。

为此，我们首先引入位移算符，以描述位置空间中坐标的变化。设任意维度位置空间中，有一态矢$| \boldsymbol{r} \rangle$，其平移任意一段无穷小的距离$d \boldsymbol{s}$后，变为另一态矢$| \boldsymbol{r}+d \boldsymbol{s} \rangle$，这一过程对应于一个算符，记为$\hat{D}(d \boldsymbol{s})$，对应的变换过程为$| \boldsymbol{r} \rangle \rightarrow | \boldsymbol{r}+d \boldsymbol{s} \rangle=\hat{D}(d \boldsymbol{s})| \boldsymbol{r} \rangle$。此时有：

$$\begin{align} \hat{\boldsymbol{r}} \hat{D}(d \boldsymbol{s}) | \boldsymbol{r} \rangle &= \hat{\boldsymbol{r}} | \boldsymbol{r}+d \boldsymbol{s} \rangle=(\boldsymbol{r}+d \boldsymbol{s}) | \boldsymbol{r}+d \boldsymbol{s} \rangle \\ \hat{D}(d \boldsymbol{s}) \hat{\boldsymbol{r}} | \boldsymbol{r} \rangle &= \hat{D}(d \boldsymbol{s}) (\boldsymbol{r} | \boldsymbol{r} \rangle)=\boldsymbol{r} \hat{D}(d \boldsymbol{s}) | \boldsymbol{r} \rangle=\boldsymbol{r} | \boldsymbol{r}+d \boldsymbol{s} \rangle \\ [\hat{\boldsymbol{r}}, \hat{D}(d \boldsymbol{s})] | \boldsymbol{r} \rangle &= [\hat{\boldsymbol{r}} \hat{D}(d \boldsymbol{s})-\hat{D}(d \boldsymbol{s}) \hat{\boldsymbol{r}}] | \boldsymbol{r} \rangle=d \boldsymbol{s} | \boldsymbol{r}+d \boldsymbol{s} \rangle \simeq d \boldsymbol{s} | \boldsymbol{r} \rangle \end{align}$$

故$[\hat{\boldsymbol{r}}, \hat{D}(d \boldsymbol{s})]=d \boldsymbol{s}$，此外，由平移的物理意义，我们希望位移算符$\hat{D}(d \boldsymbol{s})$具备以下性质：

i. $\hat{D}(d \boldsymbol{s})$不影响态矢的内积，即对任意$| \boldsymbol{r}_1\rangle$和$| \boldsymbol{r}_2 \rangle$，在平移$d \boldsymbol{s}$，变为$| \boldsymbol{r}_1^{‘} \rangle=\hat{D}(d \boldsymbol{s}) | \boldsymbol{r}_1 \rangle$和$| \boldsymbol{r}_2^{‘} \rangle=\hat{D}(d \boldsymbol{s}) | \boldsymbol{r}_2 \rangle$后，有$\langle \boldsymbol{r}_1^{‘} | \boldsymbol{r}_2^{‘} \rangle=\langle \boldsymbol{r}_1 | \hat{D}^{\dagger}(d \boldsymbol{s}) \hat{D}(d \boldsymbol{s}) | \boldsymbol{r}_2 \rangle=\langle \boldsymbol{r}_1 | \boldsymbol{r}_2 \rangle$;
推论i. $\hat{D}^{\dagger}(d \boldsymbol{s}) \hat{D}(d \boldsymbol{s})=\hat{I}$，即$\hat{D}(d \boldsymbol{s})$具有幺正性;
ii.（平移可加性）任意连续的平移操作$\hat{D}(d \boldsymbol{s}_1)$和$\hat{D}(d \boldsymbol{s}_2)$，等价于一次总平移为$d \boldsymbol{s}_1+d \boldsymbol{s}_2$的平移操作，即$\hat{D}(d \boldsymbol{s}_2) \hat{D}(d \boldsymbol{s}_1)=\hat{D}(d \boldsymbol{s}_1+d \boldsymbol{s}_2)$;
iii. （平移逆操作定义）平移的逆操作等同于沿相反方向的平移操作，即$\hat{D}^{-1}(d \boldsymbol{s})=\hat{D}(-d \boldsymbol{s})$;
iv. 当$d \boldsymbol{s}$趋近于0，$\hat{D}(d \boldsymbol{s})$趋近于单位算符$\hat{I}$.

容易验证，若取$\hat{D}(d \boldsymbol{s})=\hat{I}-\mathrm{i} \hat{\boldsymbol{K}} \cdot d \boldsymbol{s}$（$\hat{\boldsymbol{K}}$为厄米算符），并忽略高阶无穷小项，则上述性质均可满足，此时代入位移算符与坐标算符的对易关系，得

$$\begin{align} [\hat{\boldsymbol{r}}, \hat{D}(d \boldsymbol{s})] &= \hat{\boldsymbol{r}} \hat{D}(d \boldsymbol{s})-\hat{D}(d \boldsymbol{s}) \hat{\boldsymbol{r}}=\hat{\boldsymbol{r}} (\hat{I}-\mathrm{i} \hat{\boldsymbol{K}} \cdot d \boldsymbol{s})-(\hat{I}-\mathrm{i} \hat{\boldsymbol{K}} \cdot d \boldsymbol{s}) \hat{\boldsymbol{r}} \\ &= -\mathrm{i} \big[ \hat{\boldsymbol{r}} (\hat{\boldsymbol{K}} \cdot d \boldsymbol{s})-(\hat{\boldsymbol{K}} \cdot d \boldsymbol{s}) \hat{\boldsymbol{r}} \big]=d \boldsymbol{s} \end{align}$$

由于无穷小量的方向任意，因此可以令$d \boldsymbol{s}$取向与某一坐标轴重合，即$d \boldsymbol{s}=ds \boldsymbol{e}_j$，此时$\hat{\boldsymbol{K}} \cdot d \boldsymbol{s}=\hat{K}_j ds$。另一方面，将坐标算符展开，得$\hat{\boldsymbol{r}}=\sum\limits_{i=1}^{n} \hat{r}_i \boldsymbol{e}_i$，代入上式，得

$$-\mathrm{i} \big[ (\sum\limits_{i=1}^{n} \hat{r}_i \boldsymbol{e}_i) \hat{K}_j ds-\hat{K}_j ds (\sum\limits_{i=1}^{n} \hat{r}_i \boldsymbol{e}_i) \big]=\sum\limits_{i=1}^{n} (-\mathrm{i} ds \boldsymbol{e}_i) (\hat{r}_i \hat{K}_j-\hat{K}_j \hat{r}_i)=ds \boldsymbol{e}_j$$

比较左右两边可知$-\mathrm{i} [\hat{r}_i,\hat{K}_j]=\delta_{ij}$，或写作$[\hat{r}_i,\hat{K}_j]=\mathrm{i} \delta_{ij}$，再比照基本对易关系，得$\hat{K}_j=\frac{\hat{p}_j}{\hbar}$，从而平移算符表示为$\hat{D}(d \boldsymbol{s})=\hat{I}-\frac{\mathrm{i}}{\hbar} \hat{\boldsymbol{p}} \cdot d \boldsymbol{s}$。

如果位移算符作用长度不是无穷小量$d \boldsymbol{s}$，而是一段有穷长度$\boldsymbol{s}$，那么平移算符将变为

$$\hat{D}(\boldsymbol{s})=\lim_{n \rightarrow \infty} (\hat{I}-\frac{\mathrm{i}}{\hbar} \hat{\boldsymbol{p}} \cdot \frac{\boldsymbol{s}}{n})^{n}=\mathrm{e}^{-\frac{\mathrm{i}}{\hbar} \hat{\boldsymbol{p}} \cdot \boldsymbol{s}}$$

有了位移算符，我们就可以在位置表象中描述动量算符。首先，将位移算符作用于任意态矢$| u \rangle$，得$\hat{D}(d \boldsymbol{s}) | u \rangle=(\hat{I}-\frac{\mathrm{i}}{\hbar} \hat{\boldsymbol{p}} \cdot d \boldsymbol{s}) | u \rangle$，随后左乘$\langle \boldsymbol{r} |$，变为

$$\begin{align} \mathrm{left} &= \langle \boldsymbol{r} | \hat{D}(d \boldsymbol{s}) | u \rangle=\langle u | \hat{D}^{\dagger}(d \boldsymbol{s}) | \boldsymbol{r} \rangle^{*}=\langle u | \hat{D}^{-1}(d \boldsymbol{s}) | \boldsymbol{r} \rangle^{*} \\ &=\langle u | \hat{D}(-d \boldsymbol{s}) | \boldsymbol{r} \rangle^{*}=\langle u | \boldsymbol{r}-d \boldsymbol{s} \rangle^{*}=\langle \boldsymbol{r}-d \boldsymbol{s} | u \rangle \\ \mathrm{right} &= \langle \boldsymbol{r} | (\hat{I}-\frac{\mathrm{i}}{\hbar} \hat{\boldsymbol{p}} \cdot d \boldsymbol{s}) | u \rangle=\langle \boldsymbol{r} | u \rangle-\frac{\mathrm{i}}{\hbar} \langle \boldsymbol{r} | \hat{\boldsymbol{p}} | u \rangle \cdot d \boldsymbol{s} \end{align}$$

左式即为波函数$\psi(\boldsymbol{r}-d \boldsymbol{s})$，其泰勒展开为$\psi(\boldsymbol{r}-d \boldsymbol{s})=\psi(\boldsymbol{r})+\sum\limits_{i=1}^{\infty} \frac{\partial^{i} \psi}{\partial \boldsymbol{r}^{i}} (-d \boldsymbol{s})^{i}$，截断到一次项，并记$\nabla_{\boldsymbol{r}}=\frac{\partial}{\partial \boldsymbol{r}}$，得

$$\psi(\boldsymbol{r}-d \boldsymbol{s}) \simeq \psi(\boldsymbol{r})-\nabla_{\boldsymbol{r}} \psi(\boldsymbol{r}) \cdot d \boldsymbol{s}=\langle \boldsymbol{r} | u \rangle-\nabla_{\boldsymbol{r}} \langle \boldsymbol{r} | u \rangle \cdot d \boldsymbol{s}=\langle \boldsymbol{r} | u \rangle-\frac{\mathrm{i}}{\hbar} \langle \boldsymbol{r} | \hat{\boldsymbol{p}} | u \rangle \cdot d \boldsymbol{s}$$

故$\nabla_{\boldsymbol{r}} \langle \boldsymbol{r} | u \rangle=\frac{\mathrm{i}}{\hbar} \langle \boldsymbol{r} | \hat{\boldsymbol{p}} | u \rangle$，即$\langle \boldsymbol{r} | \hat{\boldsymbol{p}} | u \rangle=-\mathrm{i} \hbar \nabla_{\boldsymbol{r}} \langle \boldsymbol{r} | u \rangle$。从而在位置表象中，动量算符即为$\hat{\boldsymbol{p}}=-\mathrm{i} \hbar \nabla_{\boldsymbol{r}}$，该表达式仅在直角坐标系中成立。

[I-4] 位置空间与动量空间的转换

有了动量算符在位置表象的表示，我们可以将位置空间与动量空间的波函数进行相互转换：

$$\varphi(\boldsymbol{p})=\langle \boldsymbol{p} | u \rangle=\int \langle \boldsymbol{p} | \boldsymbol{r} \rangle d \boldsymbol{r} \langle \boldsymbol{r} | u \rangle=\int \langle \boldsymbol{p} | \boldsymbol{r} \rangle d^{n}r \langle \boldsymbol{r} | u \rangle \\ \psi(\boldsymbol{r})=\langle \boldsymbol{r} | u \rangle=\int \langle \boldsymbol{r} | \boldsymbol{p} \rangle d \boldsymbol{p} \langle \boldsymbol{p} | u \rangle=\int \langle \boldsymbol{r} | \boldsymbol{p} \rangle d^{n}p \langle \boldsymbol{p} | u \rangle$$

然而，上述转换式中出现了未知量$\langle \boldsymbol{p} | \boldsymbol{r} \rangle$和$\langle \boldsymbol{r} | \boldsymbol{p} \rangle$，这是我们亟待解决的，为此，我们考虑动量算符作用在动量态矢的表达式$\hat{\boldsymbol{p}} | \boldsymbol{p} \rangle=\boldsymbol{p} | \boldsymbol{p} \rangle$，左乘$\langle \boldsymbol{r} |$得$\langle \boldsymbol{r} | \hat{\boldsymbol{p}} | \boldsymbol{p} \rangle=-\mathrm{i} \hbar \nabla_{\boldsymbol{r}} \langle \boldsymbol{r} | \boldsymbol{p} \rangle=\boldsymbol{p} \langle \boldsymbol{r} | \boldsymbol{p} \rangle$，这是一个自变量为$\boldsymbol{r}$的微分方程，故

$$-\mathrm{i} \hbar \nabla_{\boldsymbol{r}} \langle \boldsymbol{r} | \boldsymbol{p} \rangle=\boldsymbol{p} \langle \boldsymbol{r} | \boldsymbol{p} \rangle \; \Rightarrow \; \frac{\partial \langle \boldsymbol{r} | \boldsymbol{p} \rangle}{\langle \boldsymbol{r} | \boldsymbol{p} \rangle}=\frac{\mathrm{i} \boldsymbol{p}}{\hbar} \partial \boldsymbol{r} \; \Rightarrow \; \ln{\frac{\langle \boldsymbol{r} | \boldsymbol{p} \rangle}{A}}=\frac{\mathrm{i} \boldsymbol{p} \cdot \boldsymbol{r}}{\hbar} \; \Rightarrow \; \langle \boldsymbol{r} | \boldsymbol{p} \rangle=A \mathrm{e}^{\frac{\mathrm{i} \boldsymbol{p} \cdot \boldsymbol{r}}{\hbar}} (A \in \mathbb{C})$$

根据动量空间基矢的正交归一条件，我们有

$$\begin{align} \delta^{n}(\boldsymbol{p}'-\boldsymbol{p}) &= \langle \boldsymbol{p}' | \boldsymbol{p} \rangle=\int \langle \boldsymbol{p}' | \boldsymbol{r} \rangle d^{n}r \langle \boldsymbol{r} | \boldsymbol{p} \rangle=\int A^{*} \mathrm{e}^{-\frac{\mathrm{i} \boldsymbol{p} \cdot \boldsymbol{r}}{\hbar}} \cdot A \mathrm{e}^{\frac{\mathrm{i} \boldsymbol{p} \cdot \boldsymbol{r}}{\hbar}} d^{n}r \\ &= \big| A \big|^2 \int \mathrm{e}^{\frac{\mathrm{i} (\boldsymbol{p}-\boldsymbol{p}') \cdot \boldsymbol{r}}{\hbar}} d^{n}r=\big| A \big|^2 (2 \pi \hbar)^n \cdot \frac{1}{(2 \pi \hbar)^n} \int \mathrm{e}^{\frac{-\mathrm{i} (\boldsymbol{p}'-\boldsymbol{p}) \cdot \boldsymbol{r}}{\hbar}} d^{n}r \\ &= \big| A \big|^2 (2 \pi \hbar)^n \delta^{n}(\boldsymbol{p}'-\boldsymbol{p}) \end{align}$$

因此$\big| A \big|=(2 \pi \hbar)^{-\frac{n}{2}}$，若取$A$为实数，则$\langle \boldsymbol{r} | \boldsymbol{p} \rangle=A \mathrm{e}^{\frac{\mathrm{i} \boldsymbol{p} \cdot \boldsymbol{r}}{\hbar}}=(2 \pi \hbar)^{-\frac{n}{2}} \mathrm{e}^{\frac{\mathrm{i} \boldsymbol{p} \cdot \boldsymbol{r}}{\hbar}}$

上式的推导过程中，用到狄拉克delta函数的常用表达形式$\delta(q)=\frac{1}{2 \pi} \int^{+\infty}_{-\infty} \mathrm{e}^{-\mathrm{i} kq} dq$，及以直角坐标表示的多维空间中，delta函数与一维空间的delta函数的关系$\delta^{n}(\boldsymbol{q})=\prod\limits_{i=1}^{n} \delta(q_i)$

这样，位置空间与动量空间的波函数相互转换的表达式，便可以改写为

$$\varphi(\boldsymbol{p})=\langle \boldsymbol{p} | u \rangle=\int \langle \boldsymbol{p} | \boldsymbol{r} \rangle d^{n}r \langle \boldsymbol{r} | u \rangle=(2 \pi \hbar)^{-\frac{n}{2}} \int \mathrm{e}^{-\frac{\mathrm{i} \boldsymbol{p} \cdot \boldsymbol{r}}{\hbar}} \psi(\boldsymbol{r}) d^{n}r \\ \psi(\boldsymbol{r})=\langle \boldsymbol{r} | u \rangle=\int \langle \boldsymbol{r} | \boldsymbol{p} \rangle d^{n}p \langle \boldsymbol{p} | u \rangle=(2 \pi \hbar)^{-\frac{n}{2}} \int \mathrm{e}^{\frac{\mathrm{i} \boldsymbol{p} \cdot \boldsymbol{r}}{\hbar}} \varphi(\boldsymbol{p}) d^{n}p$$

[I-5] 量子力学的角动量算符

在经典力学中，三维空间的角动量的定义为$\boldsymbol{L}=\boldsymbol{r} \times \boldsymbol{p}$，其中$\boldsymbol{r}$为圆周运动时圆心到物体的位置矢量，$\boldsymbol{p}$为物体做圆周运动时的动量。而在量子力学中，三维空间的角动量算符的定义与经典力学相近：$\hat{\boldsymbol{L}}=\hat{\boldsymbol{r}} \times \hat{\boldsymbol{p}}$——仅仅将位置和动量用对应的算符替代而已。

根据[I-5]节的介绍，在直角坐标系中，动量算符于位置空间的表达式为$\hat{\boldsymbol{p}}=-\mathrm{i} \hbar \nabla_{\boldsymbol{r}}$，对应于每一维，则有$\hat{p}_i=-\mathrm{i} \hbar \nabla_{r_i}$，将其代入角动量算符的定义，可得

$$\hat{\boldsymbol{L}}=\hat{\boldsymbol{r}} \times \hat{\boldsymbol{p}}=-\mathrm{i} \hbar \begin{vmatrix} \boldsymbol{e}_x & \boldsymbol{e}_y & \boldsymbol{e}_z \\ \hat{x} & \hat{y} & \hat{z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \end{vmatrix}=-\mathrm{i} \hbar \big[ (\hat{y} \frac{\partial}{\partial z}-\hat{z} \frac{\partial}{\partial y}) \boldsymbol{e}_x+(\hat{z} \frac{\partial}{\partial x}-\hat{x} \frac{\partial}{\partial z}) \boldsymbol{e}_y+(\hat{x} \frac{\partial}{\partial y}-\hat{y} \frac{\partial}{\partial x}) \boldsymbol{e}_z \big]$$

从而角动量在各维度的分量为

$$\hat{L}_x=-\mathrm{i} \hbar (\hat{y} \frac{\partial}{\partial z}-\hat{z} \frac{\partial}{\partial y}) \quad \hat{L}_y=-\mathrm{i} \hbar (\hat{z} \frac{\partial}{\partial x}-\hat{x} \frac{\partial}{\partial z}) \quad \hat{L}_z=-\mathrm{i} \hbar (\hat{x} \frac{\partial}{\partial y}-\hat{y} \frac{\partial}{\partial x})$$

当维度数不为3时，叉积无良性定义，因此角动量算符需改写为$\hat{\boldsymbol{L}}=\hat{\boldsymbol{r}} \wedge \hat{\boldsymbol{p}}$，其中$\wedge$为楔积符号，满足下列性质：

i. （结合律）对任意向量$\boldsymbol{a}$, $\boldsymbol{b}$和$\boldsymbol{c}$，有$(\boldsymbol{a} \wedge \boldsymbol{b}) \wedge \boldsymbol{c}=\boldsymbol{a} \wedge (\boldsymbol{b} \wedge \boldsymbol{c})$
ii. （线性）设$k_1$与$k_2$为任意常数，对任意向量$\boldsymbol{a}_1$, $\boldsymbol{a}_2$和$\boldsymbol{b}$，有

$$\scriptsize (k_1 \boldsymbol{a}_1+k_2 \boldsymbol{a}_2) \wedge \boldsymbol{b}=k_1 (\boldsymbol{a}_1 \wedge \boldsymbol{b})+k_2 (\boldsymbol{a}_2 \wedge \boldsymbol{b}) \\ \scriptsize (k_1 \boldsymbol{a}_1+k_2 \boldsymbol{a}_2) \wedge \boldsymbol{b}=k_1 (\boldsymbol{a}_1 \wedge \boldsymbol{b})+k_2 (\boldsymbol{a}_2 \wedge \boldsymbol{b})$$

iii. （交换/反交换律）对任意向量$\boldsymbol{a}$和$\boldsymbol{b}$，若其维度数为$p$与$q$，则$\boldsymbol{a} \wedge \boldsymbol{b}=(-1)^{pq} (\boldsymbol{b} \wedge \boldsymbol{a})$

由此，我们可以推出其他维度中角动量算符的表达式：

$$\begin{align} \hat{\boldsymbol{L}} &= \hat{\boldsymbol{r}} \wedge \hat{\boldsymbol{p}}=(\sum\limits_{i=1}^{n} \hat{r}_i \boldsymbol{e}_i) \wedge (\sum\limits_{i=1}^{n} \hat{p}_i \boldsymbol{e}_i)=\sum\limits_{\substack{1 \leq i<j \leq n \\ i \neq j}} (\hat{r}_i \hat{p}_j-\hat{r}_j \hat{p}_i) (\boldsymbol{e}_i \wedge \boldsymbol{e}_j) \\ &= -\mathrm{i} \hbar \sum\limits_{\substack{1 \leq i<j \leq n \\ i \neq j}} (\hat{r}_i \frac{\partial}{\partial r_j}-\hat{r}_j \frac{\partial}{\partial r_i}) (\boldsymbol{e}_i \wedge \boldsymbol{e}_j) \end{align}$$

从而角动量在各维度的分量为$\hat{L}_{ij}=\hat{r}_i \frac{\partial}{\partial r_j}-\hat{r}_j \frac{\partial}{\partial r_i}$，其中下标$[ij]$表示转动平面由坐标轴$i$与坐标轴$j$构成，且从坐标轴$i$转向坐标轴$j$。显然，三维空间的角动量算符是上述定义的特例，因

$$\begin{align} \hat{\boldsymbol{L}} &= -\mathrm{i} \hbar \Big[ (\hat{y} \frac{\partial}{\partial z}-\hat{z} \frac{\partial}{\partial y}) (\boldsymbol{e}_y \wedge \boldsymbol{e}_z)+(\hat{z} \frac{\partial}{\partial x}-\hat{x} \frac{\partial}{\partial z}) (\boldsymbol{e}_z \wedge \boldsymbol{e}_x)+(\hat{x} \frac{\partial}{\partial y}-\hat{y} \frac{\partial}{\partial x}) (\boldsymbol{e}_x \wedge \boldsymbol{e}_y) \Big] \\ &= -\mathrm{i} \hbar \Big[ \begin{vmatrix} \hat{y} & \hat{z} \\ \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \end{vmatrix} (\boldsymbol{e}_y \wedge \boldsymbol{e}_z)-\begin{vmatrix} \hat{x} & \hat{z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial z} \end{vmatrix} (\boldsymbol{e}_z \wedge \boldsymbol{e}_x)+\begin{vmatrix} \hat{x} & \hat{y} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} \end{vmatrix} (\boldsymbol{e}_x \wedge \boldsymbol{e}_y) \Big] \\ &= -\mathrm{i} \hbar \begin{vmatrix} \boldsymbol{e}_y \wedge \boldsymbol{e}_z & \boldsymbol{e}_z \wedge \boldsymbol{e}_x & \boldsymbol{e}_x \wedge \boldsymbol{e}_y \\ \hat{x} & \hat{y} & \hat{z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \end{vmatrix} \end{align}$$

比照用叉积定义的角动量算符，有$\boldsymbol{e}_x=\boldsymbol{e}_y \wedge \boldsymbol{e}_z$, $\boldsymbol{e}_y=\boldsymbol{e}_z \wedge \boldsymbol{e}_x$, $\boldsymbol{e}_z=\boldsymbol{e}_x \wedge \boldsymbol{e}_y$，均满足右手定则的定义。在接下来的篇幅中，我们将着重讨论三维空间下的角动量算符，而不再深入探讨其余维度数的情形。

依照角动量在各维度分量的表达式，我们有如下推论：

i. $[\hat{L}_i, \hat{L}_j]=\mathrm{i} \hbar \sum\limits_{k=x,y,z} \varepsilon_{ijk} \hat{L}_k$，其中$\varepsilon_{ijk}$为Levi-Civita记号，当下标$[ijk]$中有任意两数相同时，$\varepsilon_{ijk}=0$；当下标$[ijk]=[xyz],[yzx],[zxy]$时，$\varepsilon_{ijk}=1$；当下标$[ijk]=[zyx],[yxz],[xzy]$时，$\varepsilon_{ijk}=-1$;
证明：以$[\hat{L}_x, \hat{L}_y]=\mathrm{i} \hbar \hat{L}_z$为例，因$\hat{L}_{x}=\hat{y} \hat{p}_z-\hat{z} \hat{p}_y$，$\hat{L}_{y}=\hat{z} \hat{p}_x-\hat{x} \hat{p}_z$，故

$$\scriptsize \begin{align} [\hat{L}_x, \hat{L}_y] &= [\hat{y} \hat{p}_z-\hat{z} \hat{p}_y, \hat{z} \hat{p}_x-\hat{x} \hat{p}_z]=[\hat{y} \hat{p}_z, \hat{z} \hat{p}_x-\hat{x} \hat{p}_z]-[\hat{z} \hat{p}_y, \hat{z} \hat{p}_x-\hat{x} \hat{p}_z] \\ &= [\hat{y} \hat{p}_z, \hat{z} \hat{p}_x]-[\hat{y} \hat{p}_z, \hat{x} \hat{p}_z]-[\hat{z} \hat{p}_y, \hat{z} \hat{p}_x]+[\hat{z} \hat{p}_y, \hat{x} \hat{p}_z] \\ &= \hat{y} [\hat{p}_z,\hat{z} \hat{p}_x]+[\hat{y},\hat{z} \hat{p}_x] \hat{p}_z-\hat{y} [\hat{p}_z,\hat{x} \hat{p}_z]-[\hat{y},\hat{x} \hat{p}_z] \hat{p}_z \\ &\quad -\hat{z} [\hat{p}_y, \hat{z} \hat{p}_x]-[\hat{z},\hat{z} \hat{p}_x] \hat{p}_y+\hat{z} [\hat{p}_y,\hat{x} \hat{p}_z]+[\hat{z},\hat{x} \hat{p}_z] \hat{p}_y \\ &= \hat{y}[\hat{p}_z,\hat{z}] \hat{p}_x+\hat{x} [\hat{z},\hat{p}_z] \hat{p}_y=\mathrm{i} \hbar (\hat{x} \hat{p}_y-\hat{y} \hat{p}_x)=\mathrm{i} \hbar \hat{L}_z \end{align}$$

其余情形可仿照上述推导过程加以证明;
ii. $[\hat{L}_i, \hat{r}_j]=\mathrm{i} \hbar \sum\limits_{k=x,y,z} \varepsilon_{ijk} \hat{r}_k$;
证明：以$[\hat{L}_x, \hat{y}]=\mathrm{i} \hbar \hat{z}$为例，显然

$$\scriptsize \begin{align} [\hat{L}_x, \hat{y}] &= [\hat{y} \hat{p}_z-\hat{z} \hat{p}_y,\hat{y}]=[\hat{y} \hat{p}_z,\hat{y}]-[\hat{z} \hat{p}_y,\hat{y}] \\ &= \hat{y} [\hat{p}_z,\hat{y}]+[\hat{y},\hat{y}] \hat{p}_z-\hat{z} [\hat{p}_y,\hat{y}]-[\hat{z},\hat{y}] \hat{p}_y =\mathrm{i} \hbar \hat{z} \end{align}$$

其余情形可仿照上述推导过程加以证明;
iii. $[\hat{L}_i, \hat{p}_j]=\mathrm{i} \hbar \sum\limits_{k=x,y,z} \varepsilon_{ijk} \hat{p}_k$;
证明：以$[\hat{L}_x, \hat{p}_y]=\mathrm{i} \hbar \hat{p}_z$为例，显然

$$\scriptsize \begin{align} [\hat{L}_x, \hat{y}] &= [\hat{y} \hat{p}_z-\hat{z} \hat{p}_y,\hat{p}_y]=[\hat{y} \hat{p}_z,\hat{p}_y]-[\hat{z} \hat{p}_y,\hat{p}_y] \\ &= \hat{y} [\hat{p}_z,\hat{p}_y]+[\hat{y},\hat{p}_y] \hat{p}_z-\hat{z} [\hat{p}_y,\hat{p}_y]-[\hat{z},\hat{p}_y] \hat{p}_y =\mathrm{i} \hbar \hat{p}_z \end{align}$$

其余情形可仿照上述推导过程加以证明;
iv. （角动量平方算符性质）定义角动量平方算符$\hat{L}^2=\hat{\boldsymbol{L}} \cdot \hat{\boldsymbol{L}}=\hat{L}_x^2+\hat{L}_y^2+\hat{L}_z^2$，则有$[\hat{L}^2,\hat{L}_k]=0 \; (k=x,y,z)$;
证明：以$[\hat{L}^2,\hat{L}_x]=0$为例，利用推论i，我们有

$$\scriptsize \begin{align} [\hat{L}^2,\hat{L}_x] &= [\hat{L}_x^2+\hat{L}_y^2+\hat{L}_z^2,\hat{L}_x]=[\hat{L}_x^2,\hat{L}_x]+[\hat{L}_y^2,\hat{L}_x]+[\hat{L}_z^2,\hat{L}_x] \\ &= \hat{L}_y [\hat{L}_y,\hat{L}_x]+[\hat{L}_y,\hat{L}_x] \hat{L}_y+\hat{L}_z [\hat{L}_z,\hat{L}_x]+[\hat{L}_z,\hat{L}_x] \hat{L}_z \\ &= -\mathrm{i} \hbar \hat{L}_y \hat{L}_z-\mathrm{i} \hbar \hat{L}_z \hat{L}_y+\mathrm{i} \hbar \hat{L}_z \hat{L}_y+\mathrm{i} \hbar \hat{L}_y \hat{L}_z=0 \end{align}$$

其余情形可仿照上述推导过程加以证明;
v. （上升/下降算符性质）定义角动量上升算符$\hat{L}_{+}=\hat{L}_x+\mathrm{i} \hat{L}_y$，以及下降算符$\hat{L}_{-}=\hat{L}_x-\mathrm{i} \hat{L}_y$，则有(a) $[\hat{L}_z,\hat{L}_{\pm}]=\pm \hbar \hat{L}_{\pm}$; (b) $[\hat{L}^2,\hat{L}_{\pm}]=0$; (c) $[\hat{L}_{+},\hat{L}_{-}]=2 \hbar \hat{L}_z$;
证明：(a) 利用推论i，我们有

$$\scriptsize \begin{align} [\hat{L}_z,\hat{L}_{\pm}] &= [\hat{L}_z,\hat{L}_x \pm \mathrm{i} \hat{L}_y]=[\hat{L}_z,\hat{L}_x] \pm \mathrm{i} [\hat{L}_z,\hat{L}_y] \\ &=\mathrm{i} \hbar \hat{L}_y \pm \mathrm{i} \cdot (-\mathrm{i} \hbar \hat{L}_x)=\pm \hbar (\hat{L}_x \pm \mathrm{i} \hat{L}_y)=\pm \hbar \hat{L}_{\pm} \end{align}$$

(b) 利用推论iv，我们有$[\hat{L}^2,\hat{L}_{\pm}]=[\hat{L}^2,\hat{L}_x \pm \mathrm{i} \hat{L}_y]=[\hat{L}^2,\hat{L}_x] \pm \mathrm{i} [\hat{L}^2,\hat{L}_y]=0$
(c) 利用推论i，我们有

$$\scriptsize \begin{align} [\hat{L}_{+},\hat{L}_{-}] &= [\hat{L}_x+\mathrm{i} \hat{L}_y,\hat{L}_x-\mathrm{i} \hat{L}_y] \\ &= [\hat{L}_x,\hat{L}_x]+\mathrm{i} [\hat{L}_y,\hat{L}_x]-\mathrm{i} [\hat{L}_x,\hat{L}_y]+[\hat{L}_y,\hat{L}_y] \\ &= \mathrm{i} \cdot (-\mathrm{i} \hbar \hat{L}_z)-\mathrm{i} \cdot \mathrm{i} \hbar \hat{L}_z=2 \hbar \hat{L}_z \end{align}$$

[I-6] 角动量算符的本征态与本征值

回顾前一节描述的角动量算符的性质，我们发现$\hat{L}^2$与$\hat{L}_{x}$, $\hat{L}_{y}$, $\hat{L}_{z}$对易（自然，$\hat{L}^2$也与$\hat{L}_{+}$和$\hat{L}_{-}$对易），因此，我们可以用$\hat{L}^2$与角动量算符的其中一个分量$\hat{L}_{z}$的共同本征矢，作为描述相应空间的基矢。将该基矢记为$| ab \rangle$，它满足

$$\hat{L}^2 | ab \rangle=a | ab \rangle \quad \hat{L}_{z} | ab \rangle=b | ab \rangle$$

由于角动量平方算符，以及角动量分量的平方算符的本征值均不小于零，因此

$$\langle ab | (\hat{L}_x^2+\hat{L}_y^2) | ab \rangle=\langle ab | (\hat{L}^2-\hat{L}_z^2) | ab \rangle=(a-b^2) \langle ab | ab \rangle \geq 0 \cdot \langle ab | ab \rangle$$

从而$a-b^2 \geq 0$，即$a \geq b^2$，这表明对给定的$a \geq 0$，必存在$b_{\mathrm{max}}$与$b_{\mathrm{min}}$，使得$-\sqrt{a} \leq b_{\mathrm{min}} \leq b \leq b_{\mathrm{max}} \leq \sqrt{a}$，上述推导用到基矢内积不小于零的性质。

另一方面，根据上升/下降算符与$\hat{L}^2$和$\hat{L}_{z}$的对易关系，我们有

$$\hat{L}^2 \hat{L}_{\pm} | ab \rangle=([\hat{L}^2,\hat{L}_{\pm}]+\hat{L}_{\pm} \hat{L}^2) | ab \rangle=0 \cdot | ab \rangle+\hat{L}_{\pm} \hat{L}^2 | ab \rangle=a \hat{L}_{\pm} | ab \rangle \\ \hat{L}_z \hat{L}_{\pm} | ab \rangle=([\hat{L}_z,\hat{L}_{\pm}]+\hat{L}_{\pm} \hat{L}_z) | ab \rangle=\pm \hbar \hat{L}_{\pm} | ab \rangle+b \hat{L}_{\pm} | ab \rangle=(b \pm \hbar) \hat{L}_{\pm} | ab \rangle$$

因此$\hat{L}_{\pm} | ab \rangle$仍然是$\hat{L}^2$与$\hat{L}_{z}$的本征态，且本征值分别为$a$与$(b \pm \hbar)$，从而有$\hat{L}_{\pm} | ab \rangle=c_{\pm} | a,b \pm \hbar \rangle$，其中$c_{\pm}$为常数。由于$b$存在上下界，因此当上升/下降算符分别作用于$| ab_{\mathrm{max}} \rangle$和$| ab_{\mathrm{min}} \rangle$时，结果为

$$\begin{cases} \hat{L}_{+} | ab_{\mathrm{max}} \rangle=\boldsymbol{0} \\ \hat{L}_{-} | ab_{\mathrm{min}} \rangle=\boldsymbol{0} \end{cases} \; \Rightarrow \; \begin{cases} \hat{L}_{-} \hat{L}_{+} | ab_{\mathrm{max}} \rangle=\boldsymbol{0} \\ \hat{L}_{+} \hat{L}_{-} | ab_{\mathrm{min}} \rangle=\boldsymbol{0} \end{cases}$$

将上升/下降算符展开，得

$$\begin{align} \hat{L}_{-} \hat{L}_{+} &= (\hat{L}_x-\mathrm{i} \hat{L}_y) (\hat{L}_x+\mathrm{i} \hat{L}_y)=(\hat{L}_x^2+\hat{L}_y^2)+\mathrm{i} (\hat{L}_x \hat{L}_y-\hat{L}_y \hat{L}_x) \\ &= (\hat{L}^2-\hat{L}_z^2)+\mathrm{i} \cdot \mathrm{i} \hbar \hat{L}_z=\hat{L}^2-\hat{L}_z^2-\hbar \hat{L}_z \\ \hat{L}_{+} \hat{L}_{-} &= [\hat{L}_{+},\hat{L}_{-}]+\hat{L}_{-} \hat{L}_{+}=2 \hbar \hat{L}_z+(\hat{L}^2-\hat{L}_z^2-\hbar \hat{L}_z)=\hat{L}^2-\hat{L}_z^2+\hbar \hat{L}_z \end{align}$$

代入得

$$\hat{L}_{-} \hat{L}_{+} | ab_{\mathrm{max}} \rangle=(\hat{L}^2-\hat{L}_z^2-\hbar \hat{L}_z) | ab_{\mathrm{max}} \rangle=(a-b_{\mathrm{max}}^2-\hbar b_{\mathrm{max}}) | ab_{\mathrm{max}} \rangle=\boldsymbol{0} \\ \hat{L}_{-} \hat{L}_{+} | ab_{\mathrm{min}} \rangle=(\hat{L}^2-\hat{L}_z^2+\hbar \hat{L}_z) | ab_{\mathrm{min}} \rangle=(a-b_{\mathrm{min}}^2+\hbar b_{\mathrm{min}}) | ab_{\mathrm{min}} \rangle=\boldsymbol{0}$$

比照方程两边可知$a=b_{\mathrm{max}}^2+\hbar b_{\mathrm{max}}=b_{\mathrm{min}}^2-\hbar b_{\mathrm{min}}$，移项得$(b_{\mathrm{max}}+b_{\mathrm{min}})(b_{\mathrm{max}}-b_{\mathrm{min}}+\hbar)=0$，对应的方程解为$b_{\mathrm{max}}=-b_{\mathrm{min}}$或$b_{\mathrm{max}}=b_{\mathrm{min}}-\hbar$，但由于$b_{\mathrm{max}}>b_{\mathrm{min}}>b_{\mathrm{min}}-\hbar$，故符合条件的唯一解为$b_{\mathrm{max}}=-b_{\mathrm{min}}$。

之后，我们回想起上升/下降算符的作用效果：使态矢对于$\hat{L}_{z}$的本征值$b$增加/减少一个$\hbar$，因此$b_{\mathrm{max}}-b_{\mathrm{min}}$必然为整数，从而设$j$为整数或半整数，则$b_{\mathrm{max}}-b_{\mathrm{min}}=2j \hbar$，结合$b_{\mathrm{max}}=-b_{\mathrm{min}}$，便得$b_{\mathrm{max}}=j \hbar$与$b_{\mathrm{min}}=-j \hbar$（此时$b=m \hbar; m=-j,-(j-1),\dots,j-1,j$），代回本征值$a$的表达式，则$a=(j \hbar)^2+\hbar \cdot j \hbar=j(j+1) \hbar^2$。

到这里，我们得到了两个本征值的表达式，剩下尚未求出的参数，是$\hat{L}_{\pm} | ab \rangle=c_{\pm} | a,b \pm \hbar \rangle$中$c_{\pm}$的大小，而这一部分的推导过程较为简单：

$$\begin{align} &\quad \hat{L}_{\pm} | ab \rangle=c_{\pm} | a,b \pm \hbar \rangle \\ &\Rightarrow \langle ab | \hat{L}_{\pm}^{\dagger}=\langle ab | (\hat{L}_x \pm \mathrm{i} \hat{L}_y)^{\dagger}=\langle ab | (\hat{L}_x \mp \mathrm{i} \hat{L}_y)=\langle ab | \hat{L}_{\mp}=\langle a,b \pm \hbar | c_{\pm}^{*} \\ &\Rightarrow \langle ab | \hat{L}_{\mp} \hat{L}_{\pm} | ab \rangle=\langle a,b \pm \hbar | c_{\pm}^{*} \cdot c_{\pm} | a,b \pm \hbar \rangle=\big| c_{\pm} \big|^2 \\ &\Rightarrow \langle ab | (\hat{L}^2-\hat{L}_z^2 \mp \hbar \hat{L}_z) | ab \rangle=a-b^2 \mp \hbar b=\big[ j(j+1)-m(m \pm 1) \big] \hbar^2=\big| c_{\pm} \big|^2 \\ &\quad (\mathrm{Suppose \; | ab \rangle \; and \; | a,b \pm \hbar \rangle \; have \; been \; normalized.}) \end{align}$$

若$c_{\pm}$取为实数，则$c_{\pm}=\sqrt{j(j+1)-m(m \pm 1)} \hbar$。最终，角动量算符的本征态与本征值如下（为表述方便，我们将本征矢量$| ab \rangle$改写为$| jm \rangle$）：

$$\hat{L}^2 | jm \rangle=j(j+1) \hbar^2 | jm \rangle \quad \hat{L}_z | jm \rangle=m \hbar | jm \rangle \quad \hat{L}_{\pm} | jm \rangle=\sqrt{j(j+1)-m(m \pm 1)} \hbar | j,m \pm 1 \rangle$$

[I-7] 角动量算符的球坐标表示(*)

[I-5]与[I-6]节采用的是角动量算符在直角坐标下的表现形式，这种形式在描述原子或分子轨道的状态时较为不便。为此，我们可以利用原子或高对称性分子轨道的球对称性，将角动量算符改用球坐标描述。

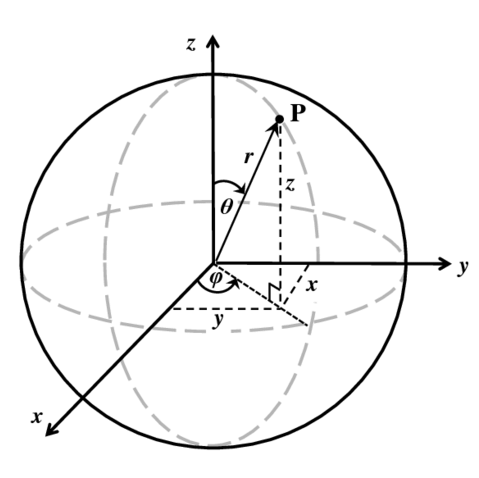
首先，我们给出两种坐标的转换公式，以及相应的全微分公式

$$\begin{align} \begin{cases} x=r \sin{\theta} \cos{\varphi} \\ y=r \sin{\theta} \sin{\varphi} \\ z=r \cos{\theta} \end{cases} \; &\Rightarrow \; \begin{cases} dx=\sin{\theta} \cos{\varphi} \; dr+r \cos{\theta} \cos{\varphi} \; d \theta-r \sin{\theta} \sin{\varphi} \; d \varphi \\ dy=\sin{\theta} \sin{\varphi} \; dr+r \cos{\theta} \sin{\varphi} \; d \theta+r \sin{\theta} \cos{\varphi} \; d \varphi \\ dz=\cos{\theta} \; dr-r \sin{\theta} \; d \theta \end{cases} \\ \begin{cases} r=\sqrt{x^2+y^2+z^2} \\ \theta=\arctan{\frac{\sqrt{x^2+y^2}}{z}} \\ \varphi=\arctan{\frac{y}{x}} \end{cases} \; &\Rightarrow \; \begin{cases} dr=\frac{x dx+y dy+zdz}{\sqrt{x^2+y^2+z^2}}=\sin{\theta} \cos{\varphi} \;dx+\sin{\theta} \sin{\varphi} \; dy+\cos{\theta} \; dz \\ d \theta=\frac{xz dx+yz dy-(x^2+y^2) dz}{(x^2+y^2+z^2) \sqrt{x^2+y^2}}=\frac{\cos{\theta} \cos{\varphi}}{r} \; dx+\frac{\cos{\theta} \sin{\varphi}}{r} \; dy-\frac{\sin{\theta}}{r} \; dz \\ d \varphi=\frac{-y dx+x dy}{x^2+y^2}=-\frac{\sin{\varphi}}{r \sin{\theta}} \; dx+\frac{\cos{\varphi}}{r \sin{\theta}} \; dy \end{cases} \end{align}$$

上述坐标表示方式对应于下图

代入角动量算符在直角坐标系下的表达式，我们有

$$\begin{align} \hat{L}_x &= -\mathrm{i} \hbar (\hat{y} \frac{\partial}{\partial z}-\hat{z} \frac{\partial}{\partial y}) \\ &= -\mathrm{i} \hbar \Big[ \hat{y} (\frac{\partial r}{\partial z} \frac{\partial}{\partial r}+\frac{\partial \theta}{\partial z} \frac{\partial}{\partial \theta}+\frac{\partial \varphi}{\partial z} \frac{\partial}{\partial \varphi})-\hat{z} (\frac{\partial r}{\partial y} \frac{\partial}{\partial r}+\frac{\partial \theta}{\partial y} \frac{\partial}{\partial \theta}+\frac{\partial \varphi}{\partial y} \frac{\partial}{\partial \varphi}) \Big] \\ &= -\mathrm{i} \hbar \Big[ r \sin{\theta} \sin{\varphi} (\cos{\theta} \frac{\partial}{\partial r}-\frac{\sin{\theta}}{r} \frac{\partial}{\partial \theta}) \\ &\quad \quad -r \cos{\theta} (\sin{\theta} \sin{\varphi} \frac{\partial}{\partial r}+\frac{\cos{\theta} \sin{\varphi}}{r} \frac{\partial}{\partial \theta}+\frac{\cos{\varphi}}{r \sin{\theta}} \frac{\partial}{\partial \varphi}) \Big] \\ &= \mathrm{i} \hbar (\sin{\varphi} \frac{\partial}{\partial \theta}+\cot{\theta} \cos{\varphi} \frac{\partial}{\partial \varphi}) \\ \hat{L}_y &= -\mathrm{i} \hbar (\hat{z} \frac{\partial}{\partial x}-\hat{x} \frac{\partial}{\partial z}) \\ &= -\mathrm{i} \hbar \Big[ \hat{z} (\frac{\partial r}{\partial x} \frac{\partial}{\partial r}+\frac{\partial \theta}{\partial x} \frac{\partial}{\partial \theta}+\frac{\partial \varphi}{\partial x} \frac{\partial}{\partial \varphi})-\hat{x} (\frac{\partial r}{\partial z} \frac{\partial}{\partial r}+\frac{\partial \theta}{\partial z} \frac{\partial}{\partial \theta}+\frac{\partial \varphi}{\partial z} \frac{\partial}{\partial \varphi}) \Big] \\ &= -\mathrm{i} \hbar \Big[ r \cos{\theta} (\sin{\theta} \cos{\varphi} \frac{\partial}{\partial r}+\frac{\cos{\theta} \cos{\varphi}}{r} \frac{\partial}{\partial \theta}-\frac{\sin{\varphi}}{r \sin{\theta}} \frac{\partial}{\partial \varphi}) \\ &\quad \quad-r \sin{\theta} \cos{\varphi} (\cos{\theta} \frac{\partial}{\partial r}-\frac{\sin{\theta}}{r} \frac{\partial}{\partial \theta}) \Big] \\ &= \mathrm{i} \hbar (-\cos{\varphi} \frac{\partial}{\partial \theta}+\cot{\theta} \sin{\varphi} \frac{\partial}{\partial \varphi}) \\ \hat{L}_z &= -\mathrm{i} \hbar (\hat{x} \frac{\partial}{\partial y}-\hat{y} \frac{\partial}{\partial x}) \\ &= -\mathrm{i} \hbar \Big[ \hat{x} (\frac{\partial r}{\partial y} \frac{\partial}{\partial r}+\frac{\partial \theta}{\partial y} \frac{\partial}{\partial \theta}+\frac{\partial \varphi}{\partial y} \frac{\partial}{\partial \varphi})-\hat{y} (\frac{\partial r}{\partial x} \frac{\partial}{\partial r}+\frac{\partial \theta}{\partial x} \frac{\partial}{\partial \theta}+\frac{\partial \varphi}{\partial x} \frac{\partial}{\partial \varphi}) \Big] \\ &= -\mathrm{i} \hbar \Big[ r \sin{\theta} \cos{\varphi} (\sin{\theta} \sin{\varphi} \frac{\partial}{\partial r}+\frac{\cos{\theta} \sin{\varphi}}{r} \frac{\partial}{\partial \theta}+\frac{\cos{\varphi}}{r \sin{\theta}} \frac{\partial}{\partial \varphi}) \\ &\quad \quad -r \sin{\theta} \sin{\varphi} (\sin{\theta} \cos{\varphi} \frac{\partial}{\partial r}+\frac{\cos{\theta} \cos{\varphi}}{r} \frac{\partial}{\partial \theta}-\frac{\sin{\varphi}}{r \sin{\theta}} \frac{\partial}{\partial \varphi}) \Big] \\ &= -\mathrm{i} \hbar \frac{\partial}{\partial \varphi} \\ \end{align}$$

进而推知

$$\begin{align} \hat{L}_{\pm} &= \hat{L}_x \pm \mathrm{i} \hat{L}_y=\mathrm{i} \hbar \Big[ (\sin{\varphi} \mp \mathrm{i} \cos{\varphi}) \frac{\partial}{\partial \theta}+(\cos{\varphi} \pm \mathrm{i} \sin{\varphi}) \cot{\theta} \frac{\partial}{\partial \varphi} \Big] \\ &= \mathrm{i} \hbar \Big[ \mp \mathrm{i} \mathrm{e}^{\pm \mathrm{i} \varphi} \frac{\partial}{\partial \theta}+\mathrm{e}^{\pm \mathrm{i} \varphi} \cot{\theta} \frac{\partial}{\partial \varphi} \Big]=\mathrm{e}^{\pm \mathrm{i} \varphi} \hbar (\pm \frac{\partial}{\partial \theta}+\mathrm{i} \cot{\theta} \frac{\partial}{\partial \varphi}) \\ \hat{L}^2 &=\hat{L}_z^2+\hbar \hat{L}_z+\hat{L}_{-} \hat{L}_{+} \\ &= -\hbar^2 \frac{\partial^2}{\partial \varphi^2}-\mathrm{i} \hbar^2 \frac{\partial}{\partial \varphi}+\mathrm{e}^{-\mathrm{i} \varphi} \hbar (-\frac{\partial}{\partial \theta}+\mathrm{i} \cot{\theta} \frac{\partial}{\partial \varphi}) \cdot \mathrm{e}^{\mathrm{i} \varphi} \hbar (\frac{\partial}{\partial \theta}+\mathrm{i} \cot{\theta} \frac{\partial}{\partial \varphi}) \\ &= -\hbar^2 \frac{\partial^2}{\partial \varphi^2}-\mathrm{i} \hbar^2 \frac{\partial}{\partial \varphi}+\hbar^2 (-\frac{\partial^2}{\partial \theta^2}+\frac{\mathrm{i}}{\sin^2{\theta}} \frac{\partial}{\partial \varphi}-\mathrm{i} \cot{\theta} \frac{\partial^2}{\partial \theta \; \partial \varphi}) \\ &\quad \quad -\hbar^2 \cot{\theta} (\frac{\partial}{\partial \theta}+\mathrm{i} \cot{\theta} \frac{\partial}{\partial \varphi})+\mathrm{i} \hbar^2 \cot{\theta} (\frac{\partial^2}{\partial \varphi \; \partial \theta}+\mathrm{i} \cot{\theta} \frac{\partial^2}{\partial \varphi^2}) \\ &= -\hbar^2 (\frac{1}{\sin^2{\theta}} \frac{\partial^2}{\partial \varphi^2}+\frac{\partial^2}{\partial \theta^2}+\cot{\theta} \frac{\partial}{\partial \theta}) \quad (\mathrm{Since} \; \frac{\partial^2}{\partial \theta \; \partial \varphi}=\frac{\partial^2}{\partial \varphi \; \partial \theta}.) \\ &= -\hbar^2 \Big[ \frac{1}{\sin^2{\theta}} \frac{\partial^2}{\partial \varphi^2}+\frac{1}{\sin{\theta}} (\sin{\theta} \frac{\partial}{\partial \theta}) \frac{\partial}{\partial \theta}+\frac{1}{\sin{\theta}} \frac{\partial (\sin{\theta})}{\partial \theta} \frac{\partial}{\partial \theta} \Big] \\ &= -\hbar^2 \Big[ \frac{1}{\sin^2{\theta}} \frac{\partial^2}{\partial \varphi^2}+\frac{1}{\sin{\theta}} \frac{\partial}{\partial \theta} (\sin{\theta} \frac{\partial}{\partial \theta}) \Big] \end{align}$$

[I-8] 角动量算符的应用——球坐标下定态薛定谔方程的求解(*)

现在，让我们采用[I-7]节的结论，求解球坐标下的定态薛定谔方程。首先，我们引入广义坐标系下梯度的表达式，

$$(q_1,q_2,\dots,q_n) \rightarrow (u_1,u_2,\dots,u_n) \\ \nabla \phi=\sum\limits_{i=1}^{n} \frac{1}{h_i} \frac{\partial \phi}{\partial u_i} \boldsymbol{e}_i \quad \nabla^2 \phi=\frac{1}{\prod\limits_{j=1}^{n} h_j} \frac{\partial}{\partial u_i} \Big( \frac{\prod\limits_{j=1}^{n} h_j}{h_i^2} \frac{\partial}{\partial u_i} \Big) \quad h_i=\sqrt{\sum\limits_{j=1}^{n} \Big( \frac{\partial q_j}{\partial u_i} \Big)^2}$$

并用此法快速写出球坐标下梯度和拉普拉斯算符的表达式：

$$\begin{align} h_r &= \sqrt{(\sin{\theta} \cos{\varphi})^2+(\sin{\theta} \sin{\varphi})^2+(\cos{\theta})^2}=1 \\ h_{\theta} &= \sqrt{(r \cos{\theta} \cos{\varphi})^2+(r \cos{\theta} \sin{\varphi})^2+(-r \sin{\theta})^2}=r \\ h_{\varphi} &= \sqrt{(-r \sin{\theta} \sin{\varphi})^2+(r \sin{\theta} \cos{\varphi})^2+0^2}=r \sin{\theta} \\ \nabla &= \frac{1}{h_r} \frac{\partial}{\partial r} \boldsymbol{e}_r+\frac{1}{h_{\theta}} \frac{\partial}{\partial \theta} \boldsymbol{e}_{\theta}+\frac{1}{h_{\varphi}} \frac{\partial}{\partial \varphi} \boldsymbol{e}_{\varphi} \\ &= \frac{\partial}{\partial r} \boldsymbol{e}_r+\frac{1}{r} \frac{\partial}{\partial \theta} \boldsymbol{e}_{\theta}+\frac{1}{r \sin{\theta}} \frac{\partial}{\partial \varphi} \boldsymbol{e}_{\varphi} \\ \nabla^2 &= \frac{1}{h_r h_{\theta} h_{\varphi}} \Big[ \frac{\partial}{\partial r} (\frac{h_{\theta} h_{\varphi}}{h_r} \frac{\partial}{\partial r})+\frac{\partial}{\partial \theta} (\frac{h_{r} h_{\varphi}}{h_{\theta}} \frac{\partial}{\partial \theta})+\frac{\partial}{\partial \varphi} (\frac{h_r h_{\theta}}{h_{\varphi}} \frac{\partial}{\partial \varphi}) \Big] \\ &= \frac{1}{1 \cdot r \cdot r \sin{\theta}} \Big[ \frac{\partial}{\partial r} (\frac{r \cdot r \sin{\theta}}{1} \frac{\partial}{\partial r})+\frac{\partial}{\partial \theta} (\frac{1 \cdot r \sin{\theta}}{r} \frac{\partial}{\partial \theta})+\frac{\partial}{\partial \varphi} (\frac{1 \cdot r}{r \sin{\theta}} \frac{\partial}{\partial \varphi}) \Big] \\ &= \frac{1}{r^2 \sin{\theta}} \Big[ 2r \sin{\theta} \frac{\partial}{\partial r}+r^2 \sin{\theta} \frac{\partial^2}{\partial r^2}+\cos{\theta} \frac{\partial}{\partial \theta}+\sin{\theta} \frac{\partial^2}{\partial \theta^2}+\frac{1}{\sin{\theta}} \frac{\partial^2}{\partial \varphi^2} \Big] \\ &= \frac{1}{r^2} \Big[ \frac{\partial}{\partial r} (r^2 \frac{\partial}{\partial r})+\frac{1}{\sin{\theta}} \frac{\partial}{\partial \theta} (\sin{\theta} \frac{\partial}{\partial \theta})+\frac{1}{\sin^2{\theta}} \frac{\partial^2}{\partial \varphi^2} \Big] \end{align}$$

接下来，我们就可以将定态薛定谔方程$\hat{H} \Psi=(-\frac{\hbar^2}{2m} \nabla^2+V) \Psi=E \Psi$用球坐标表示：

$$\begin{align} &\quad -\frac{\hbar^2}{2m} \frac{1}{r^2} \Big[ \frac{\partial}{\partial r} (r^2 \frac{\partial}{\partial r})+\frac{1}{\sin{\theta}} \frac{\partial}{\partial \theta} (\sin{\theta} \frac{\partial}{\partial \theta})+\frac{1}{\sin^2{\theta}} \frac{\partial^2}{\partial \varphi^2} \Big] \Psi(r,\theta,\varphi)+V(r,\theta,\varphi) \Psi(r,\theta,\varphi) \\ &= -\frac{\hbar^2}{2m} \frac{1}{r^2} \Big[ \frac{\partial}{\partial r} (r^2 \frac{\partial}{\partial r})-\frac{\hat{L}^2}{\hbar^2} \Big] \Psi(r,\theta,\varphi)+V(r,\theta,\varphi) \Psi (r,\theta,\varphi)=E \Psi(r,\theta,\varphi) \end{align}$$

上式将径向部分与角度部分的算符拆分，其中角度部分恰好可以用角动量平方算符描述。为进一步求解该方程，我们假定波函数的径向部分与角度部分可分离，即$\Psi(r,\theta,\varphi)=R(r) Y(\theta,\varphi)$，此时代入上式得

$$-\frac{\hbar^2}{2m} Y(\theta,\varphi) \cdot \frac{1}{r^2} \frac{\partial}{\partial r} \Big[ r^2 \frac{\partial R(r)}{\partial r} \Big]+\frac{R(r)}{2mr^2} \hat{L}^2 Y(\theta,\varphi)+V(r,\theta,\varphi) R(r) Y(\theta,\varphi)=E R(r) Y(\theta,\varphi)$$

两边除以$R(r) Y(\theta,\varphi)$，得

$$-\frac{\hbar^2}{2m} \frac{1}{R(r)} \cdot \frac{1}{r^2} \frac{\partial}{\partial r} \Big[ r^2 \frac{\partial R(r)}{\partial r} \Big]+\frac{1}{2mr^2 \cdot Y(\theta,\varphi)} \hat{L}^2 Y(\theta,\varphi)+V(r,\theta,\varphi)=E$$

由于一般情况下，势能仅是原点距离的函数，$V(r,\theta,\varphi)=V(r)$，因此移项后可变为

$$\begin{align} &\quad -\frac{\hbar^2}{2m} \frac{1}{R(r)} \cdot \frac{1}{r^2} \frac{\partial}{\partial r} \Big[ r^2 \frac{\partial R(r)}{\partial r} \Big]+V(r)-E+\frac{1}{2mr^2 \cdot Y(\theta,\varphi)} \hat{L}^2 Y(\theta,\varphi)=0 \\ &\Rightarrow \frac{1}{R(r)} \frac{\partial}{\partial r} \Big[ r^2 \frac{\partial R(r)}{\partial r} \Big]-\frac{2mr^2}{\hbar^2} \big[ V(r)-E \big]=\frac{1}{\hbar^2 Y(\theta,\varphi)} \hat{L}^2 Y(\theta,\varphi)=\lambda \end{align}$$

其中$\lambda$为常数，从而径向部分与角度部分的本征方程可分拆为

$$\frac{\partial}{\partial r} \Big[ r^2 \frac{\partial R(r)}{\partial r} \Big]-\frac{2mr^2}{\hbar^2} \big[ V(r)-E \big] R(r)=\lambda R(r) \\ \hat{L}^2 Y(\theta,\varphi)=\lambda \hbar^2 Y(\theta,\varphi)$$

沿着这一思路，我们还可以将角度部分的两个变量进行进一步拆分。记$Y(\theta,\varphi)=\Theta(\theta) \Phi(\varphi)$，则由于$[\hat{L}^2,\hat{L}_z]=0$，即$\hat{L}^2$与$\hat{L}_z$具有共同的本征态，且$\hat{L}_z=-\mathrm{i} \hbar \frac{\partial}{\partial \varphi}$，不含与$\theta$相关的算符，因此

$$\hat{L}_z Y(\theta,\varphi)=\hat{L}_z [\Theta(\theta) \Phi(\varphi)]=\Theta(\theta) \Big[ -\mathrm{i} \hbar \frac{\partial \Phi(\varphi)}{\partial \varphi} \Big]=\mu \Theta(\theta) \Phi(\varphi) \; \Rightarrow \; -\mathrm{i} \hbar \frac{\partial \Phi(\varphi)}{\partial \varphi}=\mu \Phi(\varphi)$$

上述方程的通解为$\Phi(\varphi)=\Phi(0) \mathrm{e}^{\frac{\mathrm{i} \mu}{\hbar} \varphi}$，考虑边界条件，有$\Phi(0)=\Phi(2 \pi) \neq 0 \Rightarrow \mathrm{e}^{\frac{2 \pi \mathrm{i} \mu}{\hbar}}=1$，进而$\frac{2 \pi \mathrm{i} \mu}{\hbar}=2m \pi \mathrm{i} \; (m=0,\pm 1,\pm 2,\dots)$，即$\hat{L}_z$对$\Phi(\varphi)$的本征值为$\mu=m \hbar \; (m=0,\pm 1,\pm 2,\dots)$，同时$\Phi(\varphi)=\Phi(0) \mathrm{e}^{\mathrm{i} m \varphi}$。

这样，角度部分的本征函数便改写为$Y(\theta,\varphi)=\Theta(\theta) \mathrm{e}^{\mathrm{i} m \varphi}$，我们将其代回角度部分的本征方程，并将角动量平方算符展开，得

$$\begin{align} &\quad -\hbar^2 \Big[ \frac{1}{\sin^2{\theta}} \frac{\partial^2}{\partial \varphi^2}+\frac{1}{\sin{\theta}} \frac{\partial}{\partial \theta} (\sin{\theta} \frac{\partial}{\partial \theta}) \Big] \Theta(\theta) \mathrm{e}^{\mathrm{i} m \varphi}=\lambda \hbar^2 \Theta(\theta) \mathrm{e}^{\mathrm{i} m \varphi} \\ &\Rightarrow -\hbar^2 \Big\{ -\frac{m^2 \Theta(\theta)}{\sin^2{\theta}} \mathrm{e}^{\mathrm{i} m \varphi}+\frac{1}{\sin{\theta}} \frac{\partial}{\partial \theta} \big[ \sin{\theta} \frac{\partial \Theta(\theta)}{\partial \theta} \big] \cdot \mathrm{e}^{\mathrm{i} m \varphi} \Big\}=\lambda \hbar^2 \Theta(\theta) \mathrm{e}^{\mathrm{i} m \varphi} \\ &\Rightarrow \frac{1}{\sin{\theta}} \frac{\partial}{\partial \theta} \Big[ \sin{\theta} \frac{\partial \Theta(\theta)}{\partial \theta} \Big]+\Big[ \lambda -\frac{m^2}{\sin^2{\theta}} \Big] \Theta(\theta)=0 \end{align}$$

y(x)=\Theta(\theta) \end{cases}$，则$dx=-\sin{\theta} d \theta \; (x \in [-1,1])$，$\frac{d}{d \theta}=\frac{dx}{d \theta} \frac{d}{dx}=-\sin{\theta} \frac{d}{dx}$，此时上述方程变为

$$\begin{align} &\quad \frac{1}{\sin{\theta}} \cdot (-\sin{\theta}) \frac{d}{dx} \Big[ \sin{\theta} \cdot (-\sin{\theta} \frac{dy}{dx}) \Big]+\Big[ \lambda -\frac{m^2}{1-x^2} \Big] y(x)=0 \\ &\Rightarrow \frac{d}{dx} \Big[ (1-x^2) \frac{dy}{dx} \Big]+\Big[ \lambda -\frac{m^2}{1-x^2} \Big] y=0 \\ &\Rightarrow (1-x^2) \frac{d^2 y}{dx^2}-2x \frac{dy}{dx}+\Big[ \lambda -\frac{m^2}{1-x^2} \Big] y=0 \end{align}$$

当$m=0$时，原式即为勒让德方程$(1-x^2) \frac{d^2 y}{dx^2}-2x \frac{dy}{dx}+\lambda y=0$，对$y(x)$作级数展开$y=\sum\limits_{i=0}^{\infty} c_i x^i$，则$\frac{dy}{dx}=\sum\limits_{i=1}^{\infty} i c_i x^{i-1}$，$\frac{d^2 y}{dx^2}=\sum\limits_{i=2}^{\infty} i(i-1) c_i x^{i-2}$，代入勒让德方程，有

$$\begin{align} &\quad (1-x^2) \sum\limits_{i=2}^{\infty} i(i-1) c_i x^{i-2}-2x \sum\limits_{i=1}^{\infty} i c_i x^{i-1}+\lambda \sum\limits_{i=0}^{\infty} c_i x^i=0 \\ &\Rightarrow \sum\limits_{i=0}^{\infty} (i+2)(i+1) c_{i+2} x^i-\sum\limits_{i=0}^{\infty} i(i-1) c_i x^i-\sum\limits_{i=0}^{\infty} 2i c_i x^i+\sum\limits_{i=0}^{\infty} \lambda c_i x^i=0 \\ &\Rightarrow \sum\limits_{i=0}^{\infty} \big\{ (i+2)(i+1) c_{i+2}-\big[ i(i+1)-\lambda \big] c_i \big\} x^i=0 \end{align}$$

该方程对$x \in [-1,1]$均成立，因此唯一符合要求的系数解为$c_{i+2}=\frac{i(i+1)-\lambda}{(i+2)(i+1)} c_i$，对应的线性无关的解$y(x)$为：

$$c_0 \neq 0,c_1=0 \quad y(x)=\sum\limits_{i=0}^{\infty} c_{2i} x^{2i} \\ c_0=0,c_1 \neq 0 \quad y(x)=\sum\limits_{i=0}^{\infty} c_{2i+1} x^{2i+1}$$

考虑到波函数在其定义域内必然收敛于一定值，而$x=1$时，若所有系数均不为零（即$y(x)$为无穷级数），可证明$y(x)$必然发散，矛盾！因此$y(x)$只能为截断的多项式，即在某个有限的整数$l$处，有$\frac{i(i+1)-\lambda}{(i+2)(i+1)} \Big|_{i=l}=0$，故$\lambda=l(l+1) \; (l=0,1,2,\dots)$为离散值，从而$\hat{L}^2$的本征值$l(l+1) \hbar^2$亦为离散值。

下一步是求出勒让德多项式$y(x)$（换言之，$\Theta(\theta)$）的系数，显然$c_{i+2}=\frac{i(i+1)-l(l+1)}{(i+2)(i+1)} c_i=-\frac{(l-i)(l+i+1)}{(i+2)(i+1)} c_i$，若$l$为偶数，则非零项必为偶数项，故迭代可得：

$$\begin{align} c_{2i} &= -\frac{(l-2i+2)(l+2i-1)}{2i(2i-1)} c_{2i-2} \\ &= \Big[ -\frac{(l-2i+2)(l+2i-1)}{2i(2i-1)} \Big] \cdot \Big[ -\frac{(l-2i+4)(l+2i-3)}{(2i-2)(2i-3)} \Big] c_{2i-4} \\ &= \dots =(-1)^{i} \frac{\frac{l!!}{(l-2i)!!} \frac{(l+2i-1)!!}{(l-1)!!}}{(2i)!} c_0=(-1)^{i} \frac{(\frac{l}{2})! 2^{\frac{l}{2}} \cdot (l+2i-1)!! \cdot (l+2i)!! \cdot l!!}{(2i)! \cdot (\frac{l}{2}-i)! 2^{\frac{l}{2}-i} \cdot (l-1)!! \cdot l!! \cdot (l+2i)!!} c_0 \\ &= (-1)^{i} \frac{(\frac{l}{2})! 2^{\frac{l}{2}} \cdot (l+2i)! \cdot (\frac{l}{2})! 2^{\frac{l}{2}}}{(2i)! \cdot (\frac{l}{2}-i)! 2^{\frac{l}{2}-i} \cdot l! \cdot (\frac{l}{2}+i)! 2^{\frac{l}{2}+i}} c_0=(-1)^{i} \frac{(l+2i)! \big[ (\frac{l}{2})! \big]^2}{(2i)! l! (\frac{l}{2}-i)! (\frac{l}{2}+i)!} c_0 \end{align}$$

从多项式导数的角度而言，因$\frac{d^p}{dx^p} x^{u}=\frac{u!}{(u-p)!} x^{u-p} \; (u \geq p)$，故令$2i=u-p$，$p=l$，则$\frac{d^l}{dx^l} x^{2i+l}=\frac{(2i+l)!}{(2i)!} x^{2i} \; (2i \geq 0)$，右式系数即$c_{2i}$递推式的一部分。若构造$f(x)=\frac{1}{2^{l} l!} (x^2-1)^l$，其展开后为$f(x)=\frac{1}{2^{l} l!} \sum\limits_{i=0}^{l} C_{l}^{i} (x^2)^{i} (-1)^{l-i}=\frac{1}{2^{l} l!} \sum\limits_{k=0}^{l} C_{l}^{k} (x^2)^{l-k} (-1)^{k}$，相应的$l$阶导数为

$$\begin{align} \frac{d^l f}{dx^l} &= \frac{1}{2^{l} l!} \sum\limits_{i=\frac{l}{2}}^{l} C_{l}^{i} (-1)^{l-i} \frac{d^l}{dx^l} x^{l+2i}=\frac{1}{2^{l} l!} \sum\limits_{i=0}^{\frac{l}{2}} \frac{(-1)^{\frac{l}{2}-i} l!}{(\frac{l}{2}+i)! (\frac{l}{2}-i)!} \frac{(2i+l)!}{(2i)!} x^{2i} \\ &= \frac{(-1)^{\frac{l}{2}} l!}{2^l \big[ (\frac{l}{2})! \big]^2} \sum\limits_{i=0}^{\frac{l}{2}} (-1)^{i} \frac{(l+2i)! \big[ (\frac{l}{2})! \big]^2}{(2i)! l! (\frac{l}{2}-i)! (\frac{l}{2}+i)!} x^{2i} \quad (\mathrm{since} \; (-1)^i=(-1)^{-i}) \end{align}$$

令$c_0=\frac{(-1)^{\frac{l}{2}} l!}{2^l \big[ (\frac{l}{2})! \big]^2}$，则$f(x)$的$l$阶导数即为$y(x)$的系数，由此推出勒让德方程的表达式为$P_l(x)=y(x)=\frac{1}{2^l l!} \frac{d^l}{dx^l} (x^2-1)^{l}$。以上推导过程对$l$为奇数的情形亦适用，此处不再赘述。

当$m \neq 0$时，因$x=\pm 1$处为奇点，故须考虑奇点处的渐近方程表示。令$x’=1-x$，则$dx’=-dx$，且$x’ \rightarrow 0$时，$\lambda$相对于$-\frac{m^2}{1-x^2}$可忽略，原微分方程变为

$$\begin{align} &\quad x'(2-x') \frac{d^2 y}{dx'^2}+2(1-x') \frac{dy}{dx'}-\frac{m^2}{x'(2-x')} y=0 \\ &\Rightarrow \frac{d^2 y}{dx'^2}+\frac{2(1-x')}{x'(2-x')} \frac{dy}{dx'}-\frac{m^2}{x'^2(2-x')^2} y=0 \\ &\Rightarrow \frac{d^2 y}{dx'^2}+\frac{1}{x'} \frac{dy}{dx'}-\frac{m^2}{4x'^2} y=0 \quad (\mathrm{when} \; x' \rightarrow 0) \\ \end{align}$$

令$y=(x’)^s$，则微分方程可化为

$$s(s-1)(x')^{s-2}+\frac{1}{x'} \cdot s(x')^{s-1}-\frac{m^2}{4} (x')^{s-2}=(x')^{s-2} \big[ s(s-1)+s-\frac{m^2}{4} \big]=0$$

解得$s=\pm \frac{|m|}{2}$，但若取$s=-\frac{|m|}{2}$，则$y=(x’)^s$在$x’=0$处发散，因此合理的解只能是$s=\frac{|m|}{2}$，从而$x=1$处的渐近方程为$y=(x’)^{\frac{|m|}{2}}=(1-x)^{\frac{|m|}{2}}$。同理可得，$x=-1$处的渐近方程为$y=(1+x)^{\frac{|m|}{2}}$。综合两个奇点处的渐近方程表示，我们可以写出原微分方程的通解$y=(1-x)^{\frac{|m|}{2}} (1+x)^{\frac{|m|}{2}} u(x)=(1-x^2)^{\frac{|m|}{2}} u(x)$，其中$u(x)$为一级数（可能为无穷级数，也可能为有穷的多项式），对其求导得

$$\begin{align} \frac{dy}{dx} &= \frac{|m|}{2} (1-x^2)^{\frac{|m|}{2}-1} \cdot (-2x) u(x)+(1-x^2)^{\frac{|m|}{2}} \frac{du}{dx} \\ &= -(1-x^2)^{\frac{|m|}{2}} (\frac{|m|xu}{1-x^2}-\frac{du}{dx}) \\ \frac{d^2 y}{dx^2} &= -\frac{|m|}{2} (1-x^2)^{\frac{|m|}{2}-1} \cdot (-2x) \cdot (\frac{|m|xu}{1-x^2}-\frac{du}{dx}) \\ &\quad \quad -(1-x^2)^{\frac{|m|}{2}} \Big[ \frac{|m| (1+x^2) u}{(1-x^2)^2}+\frac{|m|x}{1-x^2} \frac{du}{dx}-\frac{d^2 u}{dx^2} \Big] \\ &= (1-x^2)^{\frac{|m|}{2}} \Big[ \frac{m^2 x^2 u}{(1-x^2)^2}-\frac{|m|(1+x^2)u}{(1-x^2)^2}-\frac{2|m|x}{1-x^2} \frac{du}{dx}+\frac{d^2 u}{dx^2} \Big] \end{align}$$

从而原微分方程可变换为

$$(1-x^2) \frac{d^2 u}{dx^2}-2(|m|+1)x \frac{du}{dx}+[\lambda-|m|(|m|+1)] u=0$$

两边连续求导得

$$(1-x^2) \frac{d^3 u}{dx^3}-2(|m|+2)x \frac{d^2 u}{dx^2}+\big[ \lambda-(|m|+1)(|m|+2) \big] \frac{du}{dx}=0 \\ (1-x^2) \frac{d^4 u}{dx^4}-2(|m|+3)x \frac{d^3 u}{dx^3}+\big[ \lambda-(|m|+2)(|m|+3) \big] \frac{d^2 u}{dx^2}=0 \\ \dots \dots$$

现在将上述方程与$m \neq 0$时的连带勒让德方程对比，我们发现，$u(x)$, $\frac{du}{dx}$, $\frac{d^2 u}{dx^2}$, $\dots$分别对应于$|m|$, $|m|+1$, $|m|+2$, $\dots$时的连带勒让德方程的通解。特别的，当$|m|=0$时，连带勒让德方程即退化为勒让德方程。因此，根据前述的连带勒让德方程的递推关系，我们有$u(x)=\frac{d^{|m|}}{dx^{|m|}} P_l(x)=\frac{1}{2^l l!} \frac{d^{|m|+l}}{dx^{|m|+l}} (x^2-1)^l$，从而连带勒让德方程的通解（记为$P_l^m(x)$）为

$$P_l^m(x)=y(x)=(1-x^2)^{\frac{|m|}{2}} \frac{1}{2^l l!} \frac{d^{|m|+l}}{dx^{|m|+l}} (x^2-1)^l$$

至于$m \neq 0$时方程的本征值，由于此时的通解由$m=0$时的通解经多次求导而得，因此收敛条件与$m=0$相同，即$\hat{L}^2$的本征值为$\lambda \hbar^2=l(l+1) \hbar^2 \; (l=0,1,2,\dots)$；同时，当$|m|>l$时，$P_l^m(x)=0$，与波函数不为零矛盾，从而为保证波函数存在，$|m| \leq l$，即$\hat{L}_z$的本征值为$\mu=m \hbar \; (m=-l, -l+1, \dots, l-1, l)$。

经过以上复杂的推导后，我们最终得到$\hat{L}^2$与$\hat{L}_z$共同的本征函数$Y(\theta,\varphi)$的表达式（见下），现在只需要将其归一化，即可得到球谐函数$Y_{lm} (\theta,\varphi)$的表达式

$$\begin{align} &\quad \begin{cases} Y(\theta, \varphi)=P_l^{\pm|m|}(\cos{\theta}) \mathrm{e}^{\mathrm{i} m \varphi} \\ Y_{lm}(\theta, \varphi)=c_Y Y(\theta, \varphi) \\ \iint |Y_{lm}(\theta, \varphi)|^2 \sin{\theta} d \theta d \varphi=1 \end{cases} \\ &\Rightarrow Y_{lm}(\theta, \varphi)=(-1)^{m} \sqrt{\frac{(l-m)!}{(l+m)!} \frac{2l+1}{4 \pi}} P_l^{m}(\cos{\theta}) \mathrm{e}^{\mathrm{i} m \varphi} \quad (m \in [-l,l]) \end{align}$$

[I-9] 量子力学体系随时间的变化——时间演化算符和哈密尔顿算符

量子力学不但是（也不能仅仅是）“静”的物理理论，也是“动”的物理理论，这是由于许多物理现象不但与某时刻的状态有关，还与该时刻之前的状态有关，而从该时刻前的状态变化到该时刻的状态，便会涉及量子力学体系随时间的变化，这便是最后一部分的内容。

不过，在开始这一部分的介绍之前，我们不得不接受这样一个事实——在量子力学中，时间（更准确地说，时刻）不再被认为是物理上的可观测量，而是一个参变量，这意味着时间无法用一个厄米算符表示。不过，从某一时刻的态矢$| u(t_0) \rangle$，经一段时间后转变为另一时刻的态矢$| u(t) \rangle$，这一过程可以用厄米算符$\hat{U}(t,t_0)$（称为时间演化算符）表示，且这一过程涉及到时间（更准确地说，时刻$t_0$以及$t$的变化$\Delta t=t-t_0$）。仿照[I-3]节中位移算符的性质，我们同样可以写出$\hat{U}(t,t_0)$的性质：

i. $\hat{U}(t,t_0)$不影响态矢的内积，即对$| u(t) \rangle=\hat{U}(t,t_0) | u(t_0) \rangle$, $| v(t) \rangle=\hat{U}(t,t_0) | v(t_0) \rangle$，其内积满足$\langle v(t) | u(t) \rangle=\langle v(t_0) | \hat{U}^{\dagger}(t,t_0) \hat{U}(t,t_0) | u(t_0) \rangle=\langle v(t_0) | u(t_0) \rangle$;
ii. （时间演化的叠加）相继两段时间的演化等效于一段总时间的演化，即$\hat{U}(t_2,t_1)\hat{U}(t_1,t_0)=\hat{U}(t_2,t_0)$;
iii. 当$\Delta t=t-t_0 \rightarrow 0$时，$\hat{U}(t,t_0)$趋近于$\hat{I}$

两相对比便会发现，时间演化算符的运算性质与位移算符差别不大，唯一的区别在于，时间演化算符不具有逆运算，这与现实世界中“时间无法倒流”的现象对应（当然，如果有一天确实观测到真正意义上的时间倒流，或许时间演化算符也会有良定义……吧）。因此，时间演化算符也具有类似于位移算符的表达形式，即当$dt \rightarrow 0$时，因$\hat{H}(t_0+dt) \rightarrow \hat{H}(t_0)$，故$\hat{U}(t_0+dt,t_0)=\hat{I}-\frac{\mathrm{i}}{\hbar} \hat{H}(t_0) dt$。

接下来，我们将仅作用微元时间的时间演化算符，拓展至作用有限且非无穷小时间的情形。仿照有限位移的位移算符的表达式，我们有：

$$\hat{U}(t,t_0)=\lim_{n \rightarrow \infty} (\hat{I}-\frac{\mathrm{i}}{\hbar} \hat{H} \frac{t-t_0}{n})^n \nRightarrow \hat{U}(t,t_0)=\mathrm{e}^{-\frac{\mathrm{i}}{\hbar} \hat{H} (t-t_0)}$$

考虑到哈密尔顿算符$\hat{H}(t)$是一个随时间变化的算符，我们无法像位移算符那样，直接推出时间演化算符的表达式，事实上，只有当哈密尔顿算符不随时间变化时，$\hat{U}(t,t_0)=\mathrm{e}^{-\frac{\mathrm{i}}{\hbar} \hat{H} (t-t_0)}$才能成立。当然，如果哈密尔顿算符随时间变化，但每一时刻的哈密尔顿算符两两对易，即对于任意时刻$t_1, t_2 \in [t_0,t]$，有$[\hat{H}(t_1),\hat{H}(t_2)]=0$，则时间演化算符为$\hat{U}(t,t_0)=\mathrm{e}^{-\frac{\mathrm{i}}{\hbar} \int^{t}_{t_0} \hat{H}(t’) dt’}$。

那么，当时间演化算符作用在态矢时，会发生什么呢？以作用微元时间的时间演化算符为例，根据定义，我们有

$$\begin{align} &\quad \hat{U}(t+dt,t) | u(t) \rangle=| u(t+dt) \rangle \\ &\Rightarrow \big[ \hat{I}-\frac{\mathrm{i}}{\hbar} \hat{H}(t) dt \big] | u(t) \rangle=| u(t+dt) \rangle \\ &\Rightarrow | u(t) \rangle-\frac{\mathrm{i}}{\hbar} \hat{H}(t) dt | u(t) \rangle=| u(t+dt) \rangle \\ &\Rightarrow \hat{H}(t) | u(t) \rangle=\mathrm{i} \hbar \frac{| u(t+dt) \rangle-| u(t) \rangle}{dt} \end{align}$$

当$dt \rightarrow 0$时，上式变为$\hat{H}(t) | u(t) \rangle=\mathrm{i} \hbar \frac{\partial}{\partial t} | u(t) \rangle$，此即含时薛定谔方程。为讨论方便，在接下来的部分中，我们假设哈密尔顿算符不随时间变化，即$\hat{H}(t)=\hat{H}(0)=\hat{H}$，这样，随时间变化的便只有态矢$| u(t) \rangle$。设$t=0$时，哈密尔顿算符的本征态为$| u(t=0) \rangle=| E_i \rangle$，对应的体系总能量为$E_i$（即$\hat{H}(0) | u(0) \rangle=\hat{H} | E_i \rangle=E_i | E_i \rangle$），则经过一段时间$t$后，态矢将变为

$$| u(t) \rangle=\hat{U}(t,0) | u(0) \rangle=\mathrm{e}^{-\frac{\mathrm{i}}{\hbar} \hat{H} t} | E_i \rangle=\mathrm{e}^{-\frac{\mathrm{i}}{\hbar} E_i t} | E_i \rangle \quad (\mathrm{since} \; \mathrm{e}^{-\frac{\mathrm{i}}{\hbar} \hat{H} t}=\sum\limits_{i=0}^{\infty} \frac{(-\frac{\mathrm{i} t}{\hbar})^i \hat{H}^i}{i!})$$

故除去相位差别外，$t$时刻的态矢$| u(t) \rangle$仍是哈密尔顿算符的本征态，记该态矢为$| E_i,t \rangle$，其满足$\hat{H}(t) | E_i,t \rangle=E_i | E_i,t \rangle$。相应的，对任意力学量$\hat{F}$，其在$t$时刻的期望值$\langle \hat{F} \rangle$为

$$\langle \hat{F} \rangle(t)=\langle E_i,t | \hat{F} | E_i,t \rangle=(\langle E_i | \mathrm{e}^{\frac{\mathrm{i}}{\hbar} E_i t}) \hat{F} (\mathrm{e}^{-\frac{\mathrm{i}}{\hbar} E_i t} | E_i \rangle)=\langle E_i | F | E_i \rangle$$

故力学量$\hat{F}$的期望值不随时间的变化而改变，从而在这一意义上，能量本征态被称为定态（此处隐含一个假设：力学量$\hat{F}$不随时间的变化而改变，而态矢随时间的变化而改变。这种对体系随时间演化的诠释，称为薛定谔图景）。

更进一步的，即或$| u(0) \rangle$不是任一能量本征态的基矢，仍可将其投影至能量本征态上：$| u(0) \rangle=\sum\limits_{i} | E_i \rangle \langle E_i | u(0) \rangle$，从而经$t$时间的演化后，该矢量变为

$$| u(t) \rangle=\hat{U}(t,0) | u(0) \rangle=\mathrm{e}^{-\frac{\mathrm{i}}{\hbar} \hat{H} t} \sum\limits_{i} | E_i \rangle \langle E_i | u(0) \rangle=\sum\limits_{i} \mathrm{e}^{-\frac{\mathrm{i}}{\hbar} E_i t} | E_i \rangle \langle E_i | u(0) \rangle$$

上式表明，随着时间的流逝，$| u(t) \rangle$中各能量本征态的基矢的展开系数，将发生周期性（余弦）振荡，但其模长仍保持不变，因此，若对$| u(t) \rangle$测量能量，则得到某种能量本征值的概率仍不随时间变化而改变。

根据$| u(t) \rangle$的表达式，我们可以推出力学量$\hat{F}$在$t$时刻的期望值，以及该期望值对时间的任意阶微分：

$$\begin{align} \langle \hat{F} \rangle(t) &= \langle u(t) | \hat{F} | u(t) \rangle=\sum\limits_{i} \sum\limits_{j} \big[ \mathrm{e}^{\frac{\mathrm{i}}{\hbar} E_i t} \langle u(0) | E_i \rangle \langle E_i | \big] \hat{F} \big[ \mathrm{e}^{-\frac{\mathrm{i}}{\hbar} E_j t} | E_j \rangle \langle E_j | u(0) \rangle \big] \\ &= \sum\limits_{i} \sum\limits_{j} \langle u(0) | E_i \rangle \langle E_j | u(0) \rangle \langle E_i | \hat{F} | E_j \rangle \mathrm{e}^{-\frac{\mathrm{i}}{\hbar} (E_j-E_i) t} \\ \frac{d}{dt} \langle \hat{F} \rangle(t) &= \frac{d}{dt} \langle u(t) | \hat{F} | u(t) \rangle=\Big[ \frac{d \langle u(t) |}{dt} \Big] \hat{F} | u(t) \rangle+\langle u(t) | \hat{F} \Big[ \frac{d | u(t) \rangle}{dt} \Big] \\ &= \Big[ -\frac{1}{\mathrm{i} \hbar} \langle u(t) | \hat{H} \Big] \hat{F} | u(t) \rangle+\langle u(t) | \hat{F} \Big[ \frac{1}{\mathrm{i} \hbar} \hat{H} | u(t) \rangle \Big] \\ &= \frac{1}{\mathrm{i} \hbar} \langle u(t) | [\hat{F},\hat{H}] | u(t) \rangle \equiv \frac{1}{\mathrm{i} \hbar} \langle [\hat{F},\hat{H}] \rangle(t) \\ \frac{d^2}{dt^2} \langle \hat{F} \rangle(t) &= \frac{1}{\mathrm{i} \hbar} \frac{d}{dt} \langle [\hat{F},\hat{H}] \rangle(t)=\frac{1}{\mathrm{i} \hbar} \cdot \frac{1}{\mathrm{i} \hbar} \langle u(t) | [[\hat{F},\hat{H}],\hat{H}] | u(t) \rangle \equiv \frac{1}{(\mathrm{i} \hbar)^2} \langle [[\hat{F},\hat{H}],\hat{H}] \rangle(t) \\ &\dots \dots \\ \frac{d^n}{dt^n} \langle \hat{F} \rangle(t) &= \frac{1}{(\mathrm{i} \hbar)^n} \langle u(t) | \underbrace{[[[\hat{F},\hat{H}],\dots],\hat{H}]}_{n层对易符号} | u(t) \rangle \equiv \frac{1}{(\mathrm{i} \hbar)^n} \langle \underbrace{[[[\hat{F},\hat{H}],\dots],\hat{H}]}_{n层对易符号} \rangle(t) \end{align}$$

上述方程的特殊情形之一，便是力学量算符$\hat{F}$取为位置算符$\hat{x}$，此时位置期望值的一阶微分为

$$\begin{align} \frac{d}{dt} \langle \hat{x} \rangle(t) &= \frac{1}{\mathrm{i} \hbar} \langle [\hat{x},\hat{H}] \rangle(t)=\frac{1}{\mathrm{i} \hbar} \langle [\hat{x},\frac{\hat{p}^2}{2m}+V(\hat{x})] \rangle(t)=\frac{1}{\mathrm{i} \hbar} \big[ \langle [\hat{x},\frac{\hat{p}^2}{2m}] \rangle(t)+\langle [\hat{x},V(\hat{x})] \rangle(t) \big] \\ &= \frac{1}{\mathrm{i} \hbar} \langle (\frac{\hat{p}}{2m} [\hat{x},\hat{p}]+[\hat{x},\hat{p}] \frac{\hat{p}}{2m}) \rangle(t)=\frac{1}{\mathrm{i} \hbar} \frac{2 \mathrm{i} \hbar}{2m} \langle \hat{p} \rangle(t)=\frac{\langle \hat{p} \rangle(t)}{m} \end{align}$$

该式与牛顿力学中动量的定义式$p=mv=m \frac{dx}{dt}$具有相同的形式。此外，位置期望值的二阶微分为

$$\begin{align} \frac{d^2}{dt^2} \langle \hat{x} \rangle(t) &= \frac{1}{m} \frac{d}{dt} \langle \hat{p} \rangle(t)=\frac{1}{m} \frac{1}{\mathrm{i} \hbar} \langle [\hat{p},\hat{H}] \rangle(t)=\frac{1}{\mathrm{i} \hbar m} \langle [\hat{p},\frac{\hat{p}^2}{2m}+V(\hat{x})] \rangle(t) \\ &= \frac{1}{\mathrm{i} \hbar m} \big[ \langle [\hat{p} ,\frac{\hat{p}^2}{2m}] \rangle+\langle [\hat{p},V(\hat{x})] \rangle \big]=\frac{1}{\mathrm{i} \hbar m} \langle [\hat{p},V(\hat{x})] \rangle \end{align}$$

设$V(\hat{x})=\sum\limits_{i=0}^{\infty} v_i \hat{x}^i$，则

$$\begin{align} [\hat{p},V(\hat{x})] &= [\hat{p},\sum\limits_{i=0}^{\infty} v_i \hat{x}^i]=\sum\limits_{i=0}^{\infty} v_i [\hat{p},\hat{x}^i]=\sum\limits_{i=0}^{\infty} v_i (\hat{x} [\hat{p},\hat{x}^{i-1}]+[\hat{p},\hat{x}] \hat{x}^{i-1}) \\ &= \sum\limits_{i=0}^{\infty} v_i (\hat{x} [\hat{p},\hat{x}^{i-1}]-\mathrm{i} \hbar \hat{x}^{i-1})=\sum\limits_{i=0}^{\infty} v_i (\hat{x}^2 [\hat{p},\hat{x}^{i-2}]+\hat{x} [\hat{p},\hat{x}] \hat{x}^{i-2}-\mathrm{i} \hbar \hat{x}^{i-1}) \\ &= \sum\limits_{i=0}^{\infty} v_i (\hat{x}^2 [\hat{p},\hat{x}^{i-2}]-2 \mathrm{i} \hbar \hat{x}^{i-1})=\dots=-\mathrm{i} \hbar \sum\limits_{i=0}^{\infty} v_i i \hat{x}^{i-1}=-\mathrm{i} \hbar \frac{\partial V(\hat{x})}{\partial \hat{x}} \end{align}$$

从而位置期望值的二阶微分为$\frac{d^2}{dt^2} \langle \hat{x} \rangle(t)=-\frac{1}{m} \langle \frac{\partial V(\hat{x})}{\partial \hat{x}} \rangle$，或写作$m \frac{d^2}{dt^2} \langle \hat{x} \rangle(t)=-\langle \frac{\partial V(\hat{x})}{\partial \hat{x}} \rangle$，该方程称为艾伦
费斯特定理。

[I-10] 电子自旋在均匀磁场中的进动

在本篇的末尾，我们以电子自旋在均匀磁场中的进动作结，同时为下一篇中用量子力学阐述核磁共振的脉冲序列及其效应作铺垫。

电子是自旋数为$s=\frac{1}{2}$的费米子，其自旋磁量子数为$m_s=\pm \frac{1}{2}$，因此自旋本征态（或称$\hat{S}^2$与$\hat{S}_z$的共同本征矢）为$| s=\frac{1}{2},m_s=\frac{1}{2} \rangle$和$| s=\frac{1}{2},m_s=-\frac{1}{2} \rangle$，简记为$| s_z+ \rangle$和$| s_z- \rangle$。为书写方便，我们还可以将$| s_z+ \rangle$进一步简记为$| \alpha \rangle$，并根据自旋磁量子数的符号，称为“自旋向上”；类比可得$| s_z- \rangle$进一步简记为$| \beta \rangle$，并称为“自旋向下”。

现在，我们对电子施加一个均匀恒定的磁场$\boldsymbol{B}$，根据电动力学的经验，我们可以写出电子自旋在均匀磁场中的哈密顿算符：$\hat{H}=\boldsymbol{\hat{\mu}} \cdot \boldsymbol{B}=-\frac{g_s e}{2 m} \hat{\boldsymbol{S}} \cdot \boldsymbol{B}$，取均匀磁场方向为$z$方向，则$\hat{H}=-\frac{g_s e B}{2 m} \hat{S}_z \equiv \omega \hat{S}_z$，其中$\omega=-\frac{g_s e B}{2 m}$为电子自旋的进动频率。显然，$\hat{H}$的本征态就是$\hat{S}_z$的本征态，且相应的能量本征值为$E_{\pm}=\pm \frac{1}{2} \hbar \omega$ ，故从零时刻开始，经一段时间$t$演化，对应的演化算符为$\hat{U}(t,0)=\mathrm{e}^{-\frac{\mathrm{i}}{\hbar} \hat{H} t}=\mathrm{e}^{-\frac{\mathrm{i} \omega t}{\hbar} \hat{S}_z}$。记初始时刻（$t=0$）态矢为$| u(0) \rangle=c_{\alpha} | \alpha \rangle+c_{\beta} | \beta \rangle$，则演化$t$时后，态矢将变为

$$\begin{align} | u(t) \rangle &= \hat{U}(t,0) | u(0) \rangle=\mathrm{e}^{-\frac{\mathrm{i} \omega t}{\hbar} \hat{S}_z} (c_{\alpha} | \alpha \rangle+c_{\beta} | \beta \rangle) \\ &= c_{\alpha} \mathrm{e}^{-\frac{\mathrm{i} \omega t}{\hbar} \cdot \frac{\hbar}{2}} | \alpha \rangle+c_{\beta} \mathrm{e}^{-\frac{\mathrm{i} \omega t}{\hbar} \cdot (-\frac{\hbar}{2})} | \beta \rangle \\ &= c_{\alpha} \mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} | \alpha \rangle+c_{\beta} \mathrm{e}^{\frac{\mathrm{i} \omega t}{2}} | \beta \rangle \end{align}$$

假设电子处于能量本征态之一——自旋向上，即$| u(0) \rangle=| \alpha \rangle$，则有$c_{\alpha}=1$, $c_{\beta}=0$，故$| u(t) \rangle=\mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} | \alpha \rangle$，表明无论过多长时间，该电子在均匀磁场中均保持自旋向上的状态，改变的仅仅是矢量的相位，这一结论对于自旋向下的初态亦成立。

倘若电子不是处于能量本征态，而是处于叠加态呢？例如，电子处于$\hat{S}_x$本征态$| u(0) \rangle=| s_x+ \rangle=\frac{1}{\sqrt{2}} (| \alpha \rangle+| \beta \rangle)$，此时$c_{\alpha}=c_{\beta}=\frac{1}{\sqrt{2}}$，故演化$t$时后，态矢将变为$| u(t) \rangle=\frac{1}{\sqrt{2}} (\mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} | \alpha \rangle+\mathrm{e}^{\frac{\mathrm{i} \omega t}{2}} | \beta \rangle)$，对比电子为自旋向上的情形，我们发现，当电子处于叠加态时，随着时间的流逝，自旋向上部分与自旋向下部分的相位向相反方向演化，这将影响到电子处于每种$\hat{S}_x$本征态的概率。事实上，进一步的计算表明

$$\begin{align} P(s_x \pm,t) &= \big| \langle s_x \pm | u(t) \rangle \big|^2=\big| \frac{1}{\sqrt{2}} (\langle \alpha | \pm \langle \beta |) \cdot \frac{1}{\sqrt{2}} (\mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} | \alpha \rangle+\mathrm{e}^{\frac{\mathrm{i} \omega t}{2}} | \beta \rangle) \big|^2 \\ &= \big| \frac{1}{2} (\mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} \pm \mathrm{e}^{\frac{\mathrm{i} \omega t}{2}}) \big|^2=\Big| \frac{1}{2} \big[ (\cos{\frac{\omega t}{2}}-\mathrm{i} \sin{\frac{\omega t}{2}}) \pm (\cos{\frac{\omega t}{2}}+\mathrm{i} \sin{\frac{\omega t}{2}}) \big] \Big|^2 \\ &= \begin{cases} \cos^2{\frac{\omega t}{2}} \quad (\mathrm{for} \; | s_x+ \rangle) \\ \sin^2{\frac{\omega t}{2}} \quad (\mathrm{for} \; | s_x- \rangle) \end{cases} \end{align}$$

即处于$| s_x+ \rangle$与$| s_x- \rangle$的概率呈余弦（正弦）相关函数的形式。此外，若电子的初始自旋状态为$| s_x+ \rangle$，则演化至$t$时，各自旋角动量的分量的期望值为

$$\begin{align} \langle \hat{S}_x \rangle(t) &= \langle u(t) | \hat{S}_x | u(t) \rangle=\Big[ \frac{1}{\sqrt{2}} (\mathrm{e}^{\frac{\mathrm{i} \omega t}{2}} \langle \alpha |+\mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} \langle \beta |) \Big] \hat{S}_x \Big[ \frac{1}{\sqrt{2}} (\mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} | \alpha \rangle+\mathrm{e}^{\frac{\mathrm{i} \omega t}{2}} | \beta \rangle) \Big] \\ &= \frac{1}{2} (\mathrm{e}^{\frac{\mathrm{i} \omega t}{2}} \langle \alpha |+\mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} \langle \beta |) (\mathrm{e}^{-\frac{\mathrm{i} \omega t} {2}} \cdot \frac{\hbar}{2} | \beta \rangle+\mathrm{e}^{\frac{\mathrm{i} \omega t}{2}} \cdot \frac{\hbar}{2} | \alpha \rangle) \\ &= \frac{\hbar}{4} (\mathrm{e}^{-\mathrm{i} \omega t}+\mathrm{e}^{\mathrm{i} \omega t})=\frac{\hbar}{4} \cdot 2 \cos{\omega t}=\frac{\hbar}{2} \cos{\omega t} \\ \langle \hat{S}_y \rangle(t) &= \langle u(t) | \hat{S}_y | u(t) \rangle=\Big[ \frac{1}{\sqrt{2}} (\mathrm{e}^{\frac{\mathrm{i} \omega t}{2}} \langle \alpha |+\mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} \langle \beta |) \Big] \hat{S}_y \Big[ \frac{1}{\sqrt{2}} (\mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} | \alpha \rangle+\mathrm{e}^{\frac{\mathrm{i} \omega t}{2}} | \beta \rangle) \Big] \\ &= \frac{1}{2} (\mathrm{e}^{\frac{\mathrm{i} \omega t}{2}} \langle \alpha |+\mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} \langle \beta |) (\mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} \cdot \frac{\mathrm{i} \hbar}{2} | \beta \rangle+\mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} \cdot \frac{-\mathrm{i} \hbar}{2} | \alpha \rangle) \\ &= \frac{\mathrm{i} \hbar}{4} (\mathrm{e}^{-\mathrm{i} \omega t}-\mathrm{e}^{\mathrm{i} \omega t})=\frac{\mathrm{i} \hbar}{4} \cdot (-2 \mathrm{i} \sin{\omega t})=\frac{\hbar}{2} \sin{\omega t} \\ \langle \hat{S}_z \rangle(t) &= \langle u(t) | \hat{S}_z | u(t) \rangle=\Big[ \frac{1}{\sqrt{2}} (\mathrm{e}^{\frac{\mathrm{i} \omega t}{2}} \langle \alpha |+\mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} \langle \beta |) \Big] \hat{S}_z \Big[ \frac{1}{\sqrt{2}} (\mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} | \alpha \rangle+\mathrm{e}^{\frac{\mathrm{i} \omega t}{2}} | \beta \rangle) \Big] \\ &= \frac{1}{2} (\mathrm{e}^{\frac{\mathrm{i} \omega t}{2}} \langle \alpha |+\mathrm{e}^{-\frac{\mathrm{i} \omega t}{2}} \langle \beta |) (\mathrm{e}^{-\frac{\mathrm{i} \omega t} {2}} \cdot \frac{\hbar}{2} | \alpha \rangle+\mathrm{e}^{\frac{\mathrm{i} \omega t}{2}} \cdot \frac{-\hbar}{2} | \beta \rangle) \\ &= \frac{\hbar}{4} (1-1)=0 \end{align}$$

以上推导表明，当电子的初始自旋状态为$| s_x+ \rangle$时，自旋角动量在$x$轴（或$y$轴）的分量的期望值按照余弦（正弦）函数变化，而$z$轴分量始终为零，这与自旋角动量在$xy$平面上绕$z$轴转动的图景是一致的。

参考文献

（从略，视更新情况补充，咕咕咕）

This blog is under a CC BY-NC-SA 4.0 License
本文链接：http://chemlzh.github.io/2022/11/17/NMR-spectroscopy-under-the-perspective-of-quantum-mechanics-I/